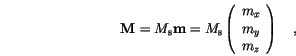2.2 Energy minimization

If the magnetization is given by

$$\mathbf{M} = M_\mathrm{s} \mathbf{m} = M_\mathrm{s} \left(... ...n{array}{c} m_x \\ m_y \\ m_z \end{array} \right) \quad,$$ (2.16)

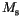where the saturation magnetization $M_\mathrm{s}$ is assumed to be constant, we get for the Landau free energy

$$G_L = E_\mathrm{exch}+E_\mathrm{ani}+E_\mathrm{ms}+E_\mathrm{ext}=$$ (2.17)

$$= \int_V \bigg\{ A \left[ (\nabla m_x)^2+(\nabla m_y)^2+(\nabla m_z)^2 \right]$$

$$-K_1 m_z^2+K_2 m_z^4$$

$$-\frac{1}{2} \mu_0 \mathbf{M} \cdot \mathbf{H}_\mathrm{ms}$$

$$- \mu_0 \mathbf{M} \cdot \mathbf{H}_\mathrm{ext} \bigg\} \,d{^3r}\, \quad.$$ (2.18)

From this equation we can calculate the Landau free energy, if the magnetization distribution within the magnetic body is known. However, in micromagnetics the task is to determine the magnetization distribution which minimizes the Landau free energy. So we need a technique to find this energy minimum and Brown [13] proposed a variational method.

He considered a small variation of the direction of the magnetization vector, rather a small variation of the magnetization distribution function by arbitrary functions. At an energy minimum the coefficients of the linear term for any choice of the variation should vanish. Proper application of this variational principle [14] finally leads to Brown's equations (in vector notation)

$$\mathbf{m} \times \left( 2A \nabla^2 \mathbf{m} + \mu_0 M... ...rtial w_\mathrm{ani}}{\partial \mathbf{m}} \right) =0 \quad.$$

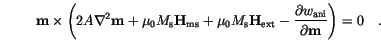
In other words, in equilibrium the magnetization is parallel to an effective field

$$\mathbf{H}_\mathrm{eff}=\frac{2A}{M_\mathrm{s}}\nabla^2 \ma... ...athrm{s}} \frac{\partial w_\mathrm{ani}}{\partial \mathbf{m}}$$ (2.19)

and the torque on the magnetization vanishes

$$\mathbf{m} \times \mathbf{H}_\mathrm{eff}=0 \quad.$$ (2.20)

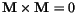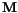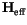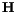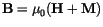Since $\mathbf{M} \times \mathbf{M} = 0$ any arbitrary vector proportional to $\mathbf{M}$ may be added to $\mathbf{H}_\mathrm{eff}$ without changing the result. It is therefore of no consequence if $\mathbf{H}$ or $\mathbf{B}=\mu_0 (\mathbf{H} + \mathbf{M})$ is used for the effective field.

Brown's equations have to be solved together with Maxwell's equations for the magnetostatic field and the proper boundary conditions. And it is necessary to check, if the solution is a minimum or a maximum, for which the variation vanishes, too. Static energy minimization using the finite element method is very efficient in calculating equilibrium magnetization distributions and nucleation fields of polycrystalline permanent magnets [15].