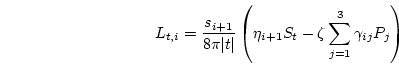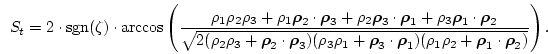


Next: 3.5 Effective Field
Up: 3. Finite Element Micromagnetics
Previous: 3.3.3 Zeeman Energy
Contents
3.4 Demagnetizing Field and Magnetostatic Energy
The demagnetizing field is a little more complicated to handle, because it is an ``open boundary problem'' with one of its boundary conditions at infinity. In order to overcome this problem Fredkin and Koehler [41,14,42] proposed a hybrid finite element/boundary element method, which requires no finite elements outside the magnetic domain  .
.
Since we assume no free currents in our system, we can calculate the demagnetizing field using a magnetic scalar potential
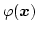 . It has to satisfy
. It has to satisfy
with the boundary conditions at the boundary 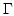 of
of 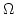
 |
(3.36) |
and
 |
(3.37) |
In addition it is required that 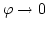 for
for
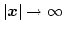 .
The weak formulation of
.
The weak formulation of
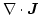 is simply given by
is simply given by
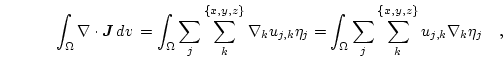 |
(3.38) |
which can again be written in matrix-vector format as
 |
(3.39) |
with
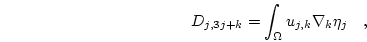 |
(3.40) |
where 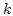 stands for the three Cartesian components
stands for the three Cartesian components 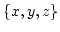 .
.
The main idea now is to split the magnetic scalar potential 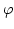 into
into 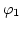 and
and 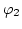 . Then the problem can be reformulated for these potentials as
. Then the problem can be reformulated for these potentials as
 |
(3.41) |
with the boundary condition
 |
(3.42) |
In addition
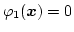 for
for
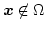 .
.
As a result, we find for 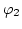
 |
(3.43) |
with
 |
(3.44) |
and
 |
(3.45) |
It is required that
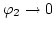 for
for
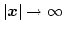 .
.
Potential theory tells us that
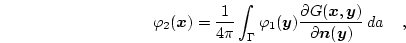 |
(3.46) |
where
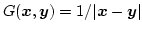 is the Green function.
is the Green function.
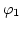 can be easily calculated using the standard finite element method as explained in Sec. 2.
can be easily calculated using the standard finite element method as explained in Sec. 2.
The (numerically expensive) evaluation of Eq. (3.46) in all 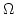 can be avoided by just calculating the boundary values of
can be avoided by just calculating the boundary values of 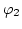 on
on 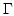 and then solving the Dirichlet problem Eq. (3.43) with the given boundary values. For
and then solving the Dirichlet problem Eq. (3.43) with the given boundary values. For
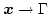 Eq. (3.46) is given by
Eq. (3.46) is given by
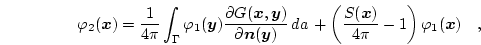 |
(3.47) |
where
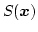 denotes the solid angle subtended by
denotes the solid angle subtended by 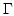 at
at
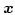 . Upon triangulation of the surface
. Upon triangulation of the surface 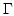 of the domain
of the domain 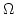 with triangular elements (which we naturally get from a triangulation of
with triangular elements (which we naturally get from a triangulation of 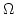 with tetrahedral elements) and discretization of
with tetrahedral elements) and discretization of 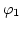 and
and 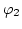 we can rewrite Eq. (3.47) as
we can rewrite Eq. (3.47) as
 |
(3.48) |
with the boundary matrix 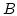 , which is a dense matrix with a size of
, which is a dense matrix with a size of
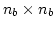 elements, where
elements, where 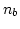 is the number of nodes on the surface
is the number of nodes on the surface 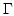 .
.
The discretization of the scalar double layer operator in Eq. (3.47) has been derived by Lindholm [43]:
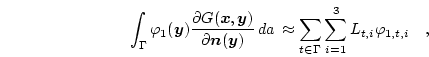 |
(3.49) |
where 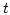 runs over all triangles on the surface
runs over all triangles on the surface 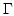 of the domain
of the domain 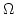 and
and 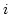 runs over the three nodes of each triangle.
runs over the three nodes of each triangle.
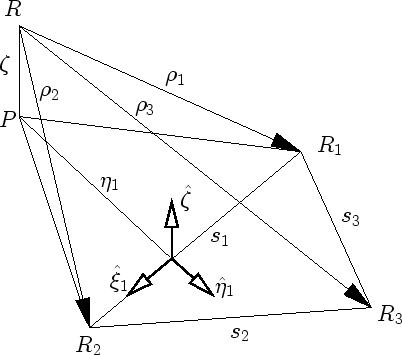
In order to calculate the matrix entries of 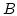 element by element (rather triangle by triangle) we use the local coordinates defined in Fig. 3.1.
element by element (rather triangle by triangle) we use the local coordinates defined in Fig. 3.1.
Figure 3.1:
Local coordinate system and various vectors required for the discretization of the boundary integral Eq. (3.47) [43].
 |
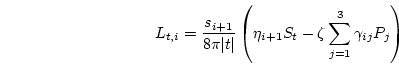 |
(3.50) |
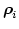 |
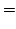 |
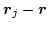 |
(3.51) |
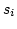 |
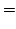 |
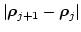 |
(3.52) |
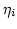 |
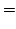 |
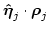 |
(3.53) |
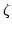 |
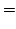 |
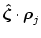 |
(3.54) |
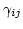 |
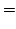 |
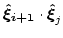 |
(3.55) |
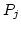 |
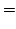 |
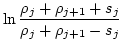 |
(3.56) |
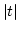 denotes the area of triangle
denotes the area of triangle 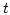 and
and 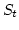 the solid angle subtended by triangle
the solid angle subtended by triangle 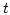 at the ``observation point''
at the ``observation point''
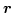 ,
which is given by
,
which is given by
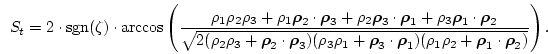 |
(3.57) |
In order to calculate the demagnetizing field, we have to perform the following steps:
Initialization
- Discretize Eq. (3.41).
- Calculate the boundary matrix in Eq. (3.48).
Solution
- Solve Eq. (3.41) for a given magnetization distribution
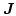 using the standard FE method.
using the standard FE method.
- Calculate
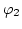 on the boundary
on the boundary 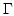 using Eq. (3.48) to get the values for the Dirichlet boundary conditions.
using Eq. (3.48) to get the values for the Dirichlet boundary conditions.
- Calculate
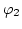 in the whole domain
in the whole domain 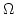 using Eq. (3.43) with Dirichlet boundary values.
using Eq. (3.43) with Dirichlet boundary values.
- Calculate
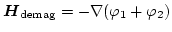 .
.



Next: 3.5 Effective Field
Up: 3. Finite Element Micromagnetics
Previous: 3.3.3 Zeeman Energy
Contents
Werner Scholz
2003-06-08
![]() .
.
![]() . It has to satisfy
. It has to satisfy
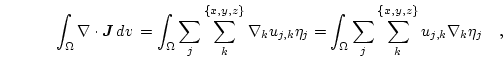
![]() into
into ![]() and
and ![]() . Then the problem can be reformulated for these potentials as
. Then the problem can be reformulated for these potentials as
![]()
![]() can be easily calculated using the standard finite element method as explained in Sec. 2.
can be easily calculated using the standard finite element method as explained in Sec. 2.
![]() can be avoided by just calculating the boundary values of
can be avoided by just calculating the boundary values of ![]() on
on ![]() and then solving the Dirichlet problem Eq. (3.43) with the given boundary values. For
and then solving the Dirichlet problem Eq. (3.43) with the given boundary values. For
![]() Eq. (3.46) is given by
Eq. (3.46) is given by
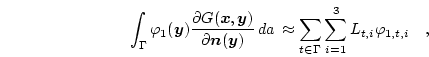
![]() element by element (rather triangle by triangle) we use the local coordinates defined in Fig. 3.1.
element by element (rather triangle by triangle) we use the local coordinates defined in Fig. 3.1.