


Next: 9.2.2 Numerical Finite Element
Up: 9.2 Analytical and Numerical
Previous: 9.2 Analytical and Numerical
Contents
The rigid vortex model assumes a ``rigid vortex'', which does not
change its shape in an external field. Together with a certain
magnetization distribution it gives an approximation for the
magnetization distribution of a curling state (vortex state) in a
fine cylindrical particle. An analytical model for the
magnetization distribution
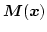 in zero field has been
developed using a variational principle by Usov and
coworkers [113,114]. It is split into two parts (cf. Fig. 9.2)
in zero field has been
developed using a variational principle by Usov and
coworkers [113,114]. It is split into two parts (cf. Fig. 9.2)
Figure 9.2:
Geometry of a flat cylindrical nanodot.
![\includegraphics[scale=0.5]{fig/papers/icfpm02/fig/dotgeom.eps}](img568.png) |
The first part describes the
magnetization in the core of the vortex (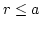 ,
, 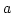 is the
vortex core radius), which is defined by
is the
vortex core radius), which is defined by 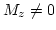 :
:
where 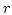 ,
, 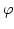 are the polar coordinates. The other part
describes the magnetization outside the core (
are the polar coordinates. The other part
describes the magnetization outside the core (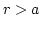 ):
):
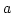 denotes the radius of the core and it is given by
denotes the radius of the core and it is given by
where 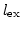 (the exchange length) is given by
(the exchange length) is given by
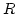 is the radius of the nanodot,
is the radius of the nanodot, 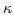 is a numerical constant (cf. [113]) and
is a numerical constant (cf. [113]) and 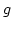 is the ratio
is the ratio 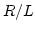 , where
, where 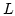 is the height of the nanodot. For permalloy we find
is the height of the nanodot. For permalloy we find
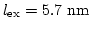 and with
and with
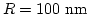 and
and
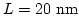 we get
we get
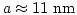 . The core radius is obtained from the minimization of the total energy (exchange and magnetostatic energy).
. The core radius is obtained from the minimization of the total energy (exchange and magnetostatic energy).
There are some typical properties of the rigid vortex model with Usov's magnetization distribution:
- In equilibrium in zero field there are surface charges only on the top and bottom surface within the vortex core.
- For shifted vortices surface charges are induced on the circumference of the nanodot.
- There are no volume charges in the model.



Next: 9.2.2 Numerical Finite Element
Up: 9.2 Analytical and Numerical
Previous: 9.2 Analytical and Numerical
Contents
Werner Scholz
2003-06-08
![]() in zero field has been
developed using a variational principle by Usov and
coworkers [113,114]. It is split into two parts (cf. Fig. 9.2)
in zero field has been
developed using a variational principle by Usov and
coworkers [113,114]. It is split into two parts (cf. Fig. 9.2)
![]() ,
, ![]() is the
vortex core radius), which is defined by
is the
vortex core radius), which is defined by ![]() :
:

