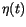6.1 Gaussian white noise

It is assumed that the thermal activation is caused by perturbations of very high frequency. ``Very high'' means in this case that the frequency is well above the typical precession frequency of the magnetization vector. Thus, the fluctuating field, which is used to simulate the effect of thermal activation, is represented by a stochastic process. It is assumed to be Gaussian white noise, because the fluctuations emerge from the interaction of the magnetization with a large number of independent microscopic degrees of freedom with equivalent stochastic properties (eg. phonons, conducting electrons, nuclear spins, etc.) [39]. As a result of the central limit theorem, the fluctuation field is Gaussian distributed.

A stochastic process 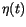$\eta(t)$ is called Gaussian white noise [40], if its time average is zero

$$\langle {\eta(t)} \rangle = 0$$

and the two time covariance function is given by

$$\langle {\eta(t)\eta(t+\tau)} \rangle = \sigma^2 \delta(\tau) \quad.$$ (6.1)

For the Fourier transform of the stationary two time covariance function we obtain

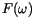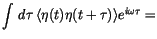$$F(\omega) = \int \,d{\tau}\, \langle {\eta(t)\eta(t+\tau)} \rangle e^{i\omega\tau} =$$ (6.2)

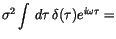$$= \sigma^2 \int \,d{\tau}\, \delta(\tau) e^{i\omega\tau} =$$ (6.3)

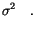$$= \sigma^2 \quad.$$ (6.4)

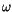In other words it does not depend on $\omega$, because there is no correlation in time. This is why it is called ``white'' noise.