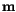Dimensionless equations

For the implementation of the finite difference model all physical quantities have been converted to dimensionless values.

The magnetization vectors 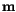$\bf m$ of the computational cells are dimensionless unit vectors

$$\mathbf{m}=\mathbf{M}/M_\mathrm{s} \quad.$$

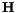The magnetic field $\bf H$ is converted by

$$\mathbf{h}=\frac{\mathbf{H}}{M_\mathrm{s}}$$

and the time is rescaled by

$$t'=t M_\mathrm{s} \gamma$$

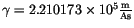where $\gamma=2.210173\times 10^{5} \frac{\mathrm{m}}{\mathrm{As}}$ is the gyromagnetic ratio.

Thus, the Landau-Lifshitz-Gilbert equation () can be rewritten as

$$\frac{d \bf m}{dt'} = -\mathbf{m}\times\mathbf{h} - \alpha \mathbf{m}\times(\mathbf{m}\times\mathbf{h}) \quad.$$

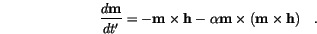
The contributions to the local magnetic field are rescaled by the material constants.

Anisotropy field

$$\mathbf{h}_\mathrm{ani}=k \mathbf{a}(\mathbf{m} \cdot \mathbf{a})\quad,\qquad k=\frac{2 K_1}{\mu_0 M_\mathrm{s}^2}$$

Exchange field

$$\mathbf{h}_\mathrm{exch}=\sum^{NN}_j a \mathbf{m}_j\quad,\qquad a=\frac{2 A}{\Delta x^2 M_\mathrm{s}^2}$$

Dipole field

$$\mathbf{h}_\mathrm{dip}=-\frac{1}{4\pi} \sum_j{}' \frac{\m... ...r}_j)}{r_j^5}\quad,\qquad \mathbf{r}_j=\mathbf{R}_j/ \Delta x$$

Thermal field

$$\mathbf{h}_\mathrm{th}= \eta \sqrt{ 2 \frac{\alpha}{1+\alpha^2} \frac{k_B T}{\Delta x^3 M^2_\mathrm{s} \Delta t'} }$$

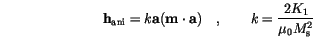
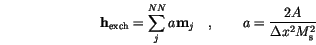
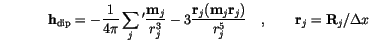
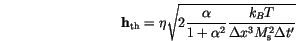
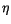$\eta$ denotes a standard Gaussian stochastic process with mean zero and variance 1.