When a regular triangulation ![]() has been generated for the domain
has been generated for the domain ![]() , the space
, the space ![]() of the numerical solution
of the numerical solution ![]() has to be defined. A common choice of
basis functions for the spline spaces
has to be defined. A common choice of
basis functions for the spline spaces ![]() and
and ![]() are ``hat functions'' (Fig. 2.2), which are defined for every node
are ``hat functions'' (Fig. 2.2), which are defined for every node ![]() of the finite element mesh as
of the finite element mesh as
| (2.19) |
| (2.20) |
| (2.21) |
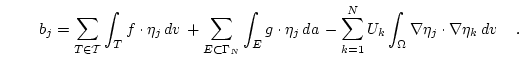 |
(2.22) |
It is most convenient to calculate the stiffness matrix on an element by element basis (local or element matrices) and finally assemble the contributions from the local matrices to the global stiffness matrix.
If we assume that the four vertices of a tetrahedral element ![]() are given by
are given by ![]() with
with
![]() , then the volume
, then the volume ![]() of the element is given by
of the element is given by
The corresponding basis functions are given by
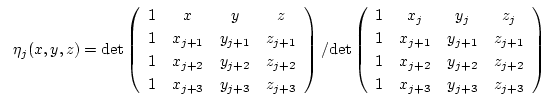 |
(2.24) |
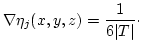 | |||
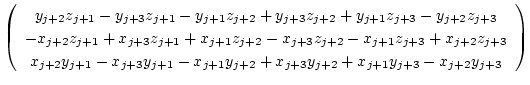 |
|||
As a result we can easily calculate the stiffness matrix entries
| (2.25) |
For the right hand side of Eq. (2.16) we need to evaluate
![]() . If we use the value of
. If we use the value of ![]() in the center of gravity
in the center of gravity ![]() of
of ![]() , we can make the approximation
, we can make the approximation
| (2.26) |
Finally, the Dirichlet boundary conditions have to be incorporated. One straight forward and easy to implement method is to replace all rows of the stiffness matrix ![]() , which correspond to Dirichlet boundary nodes, with zero and a single one in the main diagonal. On the right hand side, the entries of the Dirichlet nodes are replaced with their boundary values.
, which correspond to Dirichlet boundary nodes, with zero and a single one in the main diagonal. On the right hand side, the entries of the Dirichlet nodes are replaced with their boundary values.