


Next: 3.3.1 Exchange Energy
Up: 3. Finite Element Micromagnetics
Previous: 3.2 Gilbert Equation of
Contents
3.3 Discretization
In the following sections we will discretize the contributions to the total energy with the finite element method as shown in Sec. 2. For static energy minimization methods as well as for the calculation of the effective field Eq. (3.14)
we have to calculate the derivative of the total energy with respect to the local magnetic polarization
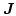 . In the following sections we will also derive these gradients.
. In the following sections we will also derive these gradients.
First we have to define the discrete approximation of the magnetic polarization
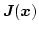 (Eq. (3.2)) by
(Eq. (3.2)) by
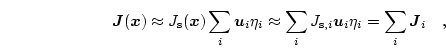 |
(3.10) |
where 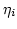 denotes the basis function (hat function) at node
denotes the basis function (hat function) at node 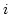 of the finite element mesh. The material parameters
of the finite element mesh. The material parameters 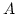 ,
, 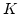 , and
, and 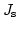 are defined element by element and they are assumed to be constant within each element. However, the magnetic polarization which depends on the saturation polarization
are defined element by element and they are assumed to be constant within each element. However, the magnetic polarization which depends on the saturation polarization 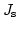 is defined on the nodes. Thus, we have to introduce the node based discrete approximation
is defined on the nodes. Thus, we have to introduce the node based discrete approximation
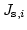 of the saturation polarization
of the saturation polarization
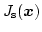 as
as
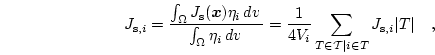 |
(3.11) |
where 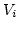 denotes the volume, which is assigned to node
denotes the volume, which is assigned to node 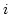 of the mesh. It is given by
of the mesh. It is given by
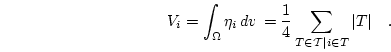 |
(3.12) |
Since
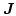 is a vector with three Cartesian components we have three times the number of nodes unknowns to calculate.
is a vector with three Cartesian components we have three times the number of nodes unknowns to calculate.
For a given basis  the total energy can be expanded as
the total energy can be expanded as
 |
(3.13) |
and we get for the effective field using the box scheme [40]
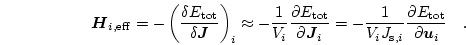 |
(3.14) |
Subsections



Next: 3.3.1 Exchange Energy
Up: 3. Finite Element Micromagnetics
Previous: 3.2 Gilbert Equation of
Contents
Werner Scholz
2003-06-08
![]() . In the following sections we will also derive these gradients.
. In the following sections we will also derive these gradients.
![]() (Eq. (3.2)) by
(Eq. (3.2)) by
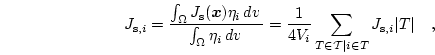
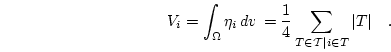
![]() the total energy can be expanded as
the total energy can be expanded as