Die Geschichte der Approximationen der Zahl 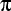
Fachbereichsarbeit aus Mathematik
eingereicht von Werner Scholz 8.A
betreut durch Mag. Ingrid Breyer
1993/94
GRG XIII Wenzgasse 7
 | |
| |
| 1. | Vorwort |
| 2. | Das Altertum |
| 2.1. | Ägypten |
| 2.2. | Babylonien |
| 2.3. | Bibel (ca. 550 v.Chr.) und Talmud (ca. 500 v.Chr.) |
| 2.4. | Indien |
| 2.5. | Griechenland |
| 2.5.1. | Hippias von Elis (ca. 425 v.Chr.) |
| 2.5.2. | Hippokrates von Chios (5. Jhdt. v.Chr.) |
| 2.5.3. | Archimedes (287 - 212 v. Chr.) |
| 3. | Mittelalter |
| 3.1. | China |
| 3.2. | Indien |
| 3.3. | Arabien |
| 3.4. | Mitteleuropa |
| 3.4.1. | Nikolaus von Kues (1401-1464) |
| 4. | Neuzeit |
| 4.1. | Gottfried Wilhelm Leibniz (1646-1716) |
| 4.2. | John Wallis (1616-1703) |
| 4.3. | John Machin (1680-1751) |
| 4.4. | Leonard Euler (1707-1783) |
| 4.5. | Weitere Berechnungen |
| 5. | Das 20. Jahrhundert |
| 5.1. | Monte-Carlo-Methoden |
| 5.1.1. | Das Buffon'sche Nadelproblem |
| 5.1.2. | Wie man |
| 6. | Kuriositäten und ein Paradoxon |
| 6.1. | Untersuchung der Ziffernfolge von |
| 6.1.1. | Magische Quadrate |
| 6.1.2. | Kreiszahl und "Kreisbuchstaben" |
| 6.2. | Das Geheimnis der Ziffernfolge |
| 7. | Reihen und Produkte zur Approximation von |
| 8. | Meilensteine in der Berechnung von |
| 9. | Zusammenfassung |
| 10. | Anhang |
| 11. | Bibliographie |
Die Idee zum Thema dieser Fachbereichsarbeit kam mir bei der Suche nach
einem geeigneten Inhalt eines Referats für das Wahlpflichtfach Mathematik.
Ich hatte zwar im Schulunterricht schon gehört, daß sich Mathematiker
seit vielen Jahrhunderten mit der Zahl ![]() beschäftigen, und noch viel öfter mit dieser Zahl gerechnet,
doch was wirklich für ein Aufwand hinter der Berechnung von
beschäftigen, und noch viel öfter mit dieser Zahl gerechnet,
doch was wirklich für ein Aufwand hinter der Berechnung von ![]() steckte, war mir verborgen geblieben. So machte ich es mir zur Aufgabe,
dieses Thema in meinem Referat etwas genauer zu beleuchten.
steckte, war mir verborgen geblieben. So machte ich es mir zur Aufgabe,
dieses Thema in meinem Referat etwas genauer zu beleuchten.
Auf die Möglichkeit, dieses Referat zu einer Fachbereichsarbeit auszubauen, machte mich erst meine Mathematikprofessorin Frau Mag. Ingrid Breyer aufmerksam. Ich möchte ihr an dieser Stelle herzlich dafür danken, daß sie mich auf diese Idee brachte, mir die Abfassung meiner ersten kleinen wissenschaftlichen Arbeit ermöglichte und mir dabei stets hilfreich und ermunternd zur Seite stand.
Weiters möchte ich Herrn Univ.-Prof. Mag. Dr. Hans-Christian
Reichel danken, daß er mich auf einen Großteil des verwendeten
Materials aufmerksam machte und mir selbiges zur Verfügung stellte,
sodaß ich aus dem vollen schöpfen konnte und Zugang zu vielen
Arbeiten über ![]() erhielt, die mir
sonst verborgen geblieben wären.
erhielt, die mir
sonst verborgen geblieben wären.
Auch meinen Eltern möchte ich meinen Dank dafür aussprechen, daß sie mir einerseits die Ausstattung mit einem PC, auf dem ich diese Fachbereichsarbeit erstellen konnte, zur Verfügung stellten und andererseits viel Zeit geschenkt haben, damit ich auch in Ruhe meine Arbeit fertigstellen konnte.
In dieser Fachbereichsarbeit wird die Geschichte der Approximationen
der Zahl ![]() , d.h. die im Laufe der Zeit
immer genauere Bestimmung des Werts von
, d.h. die im Laufe der Zeit
immer genauere Bestimmung des Werts von ![]() beschrieben. Bedeutende Mathematiker und ihre Methoden werden dabei (möglichst
in chronologischer Reihenfolge) präsentiert, sofern das mit dem mathematischen
"Handwerkszeug" eines Schülers der 8. Klasse möglich
und nachvollziehbar ist. Der Bogen spannt sich dabei vom antiken Ägypten
bis ins Computerzeitalter des 20. Jahrhunderts, wobei die Arbeit durch
zwei Computerprogramme und zwei Tabellen mit Termen zur Approximation von
beschrieben. Bedeutende Mathematiker und ihre Methoden werden dabei (möglichst
in chronologischer Reihenfolge) präsentiert, sofern das mit dem mathematischen
"Handwerkszeug" eines Schülers der 8. Klasse möglich
und nachvollziehbar ist. Der Bogen spannt sich dabei vom antiken Ägypten
bis ins Computerzeitalter des 20. Jahrhunderts, wobei die Arbeit durch
zwei Computerprogramme und zwei Tabellen mit Termen zur Approximation von
![]() und zur Geschichte der Näherungen
abgerundet wird.
und zur Geschichte der Näherungen
abgerundet wird.
Die Geschichte der Approximationen von ![]() ist über 4000 Jahre alt (vgl. Peitgen 1992, S.172f.), und erste
Ergebnisse wurden in Ägypten schon um 1850 v.Chr. im "Moskauer
Papyrus" und um 1650 v.Chr. im "Papyrus Rhind" schriftlich
festgehalten. Man fand beispielsweise die Näherung
ist über 4000 Jahre alt (vgl. Peitgen 1992, S.172f.), und erste
Ergebnisse wurden in Ägypten schon um 1850 v.Chr. im "Moskauer
Papyrus" und um 1650 v.Chr. im "Papyrus Rhind" schriftlich
festgehalten. Man fand beispielsweise die Näherung ![]() . Letzterer Papyrus enthält in Hieroglyphenschrift Aufgabentexte des
Schreibers Ahmes zur Geometrie, wobei in der 50. Aufgabe die Behauptung
aufgestellt wird, daß ein Quadrat, dessen Seitenlänge um
. Letzterer Papyrus enthält in Hieroglyphenschrift Aufgabentexte des
Schreibers Ahmes zur Geometrie, wobei in der 50. Aufgabe die Behauptung
aufgestellt wird, daß ein Quadrat, dessen Seitenlänge um ![]() kürzer sei als der Durchmesser eines Kreises, denselben Flächeninhalt
habe wie dieser.
kürzer sei als der Durchmesser eines Kreises, denselben Flächeninhalt
habe wie dieser.
In moderner Schreibweise bedeutet das: 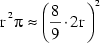
Vereinfachen bringt: 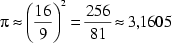
MAX BAUER (1927/28, S.3) vermutet, daß die Idee für diese Beziehung dem Vergleich von wassergefüllten zylindrischen und quaderförmigen Behältern entsprungen sein könnte. Das Produkt aus der Höhe des Wasserspiegels (bei derselben Wassermenge in den Gefäßen) und der jeweiligen Grundfläche muß gleich sein, sodaß man aus dem Verhältnis der Höhen das Verhältnis der Grundflächen der Gefäße berechnen kann.
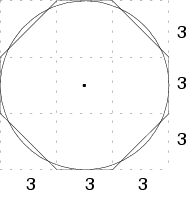
Eine zweite Herleitung, die dem 48. Problem des Schreibers Ahmes im Papyrus
Rhind entspricht, führt folgendermaßen zur selben Näherung
(vgl. Mäder 1989, S.50f.):
Der in der Skizze erkennbare Kreis hat den Radius ![]() . Sein Flächeninhalt beträgt ungefähr
. Sein Flächeninhalt beträgt ungefähr ![]() , da der Kreis von fünf Quadraten mit dem Flächeninhalt
, da der Kreis von fünf Quadraten mit dem Flächeninhalt ![]() und vier Dreiecken mit dem Flächeninhalt
und vier Dreiecken mit dem Flächeninhalt ![]() annähernd ausgefüllt wird. Die Formel für den Flächeninhalt
war den ägyptischen Mathematikern schon bekannt, sodaß sich
daraus ergibt:
annähernd ausgefüllt wird. Die Formel für den Flächeninhalt
war den ägyptischen Mathematikern schon bekannt, sodaß sich
daraus ergibt:
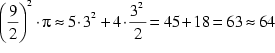
Daraus folgt: 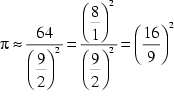
Es könnte aber auch schon vor der Abfassung des Papyrus Rhind bessere Approximationen gegeben haben: POSAMENTIER (The Mathematics Teacher v. 77(1); S.52,47) führt das Buch "La Science Mystérieuse des Pharaons" von Abbé Moreux (Paris 1923) an, wo auf den Seiten 28-29 eine vermutete Näherung von 3,14159294 angegeben wird. (zitiert nach Mäder 1989, S.55)
Ungefähr zur selben Zeit (1900-1600 v.Chr.) gab es auch schon in
Babylonien erste Approximationen für ![]() .
Eine solche Näherung stellte der Wert 3 dar. Dieser könnte durch
Einschreiben eines 12-Ecks in den Einheitskreis entstanden sein: (Diese
Annahme stammt aus dem "Telekolleg II Mathematik" des Bayerischen
Rundfunks und des Südwest 3. In der am 6. Juli 1993 ausgestrahlten
Sendung wurde diese Idee präsentiert.)
.
Eine solche Näherung stellte der Wert 3 dar. Dieser könnte durch
Einschreiben eines 12-Ecks in den Einheitskreis entstanden sein: (Diese
Annahme stammt aus dem "Telekolleg II Mathematik" des Bayerischen
Rundfunks und des Südwest 3. In der am 6. Juli 1993 ausgestrahlten
Sendung wurde diese Idee präsentiert.)
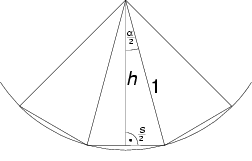
Wie man in der Zeichnung erkennt, gelten die beiden Beziehungen:
![]() und
und 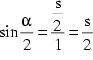
Da im 12-Eck ![]() ist, errechnet sich der Flächeninhalt des 12-Ecks dann folgendermaßen:
ist, errechnet sich der Flächeninhalt des 12-Ecks dann folgendermaßen:
![]()
Damit wäre ![]() durch den Wert 3
approximiert.
durch den Wert 3
approximiert.
Keilschrifttexte, die 1936 in Susa entdeckt wurden, führen für
![]() den Wert
den Wert ![]() an. (vgl. Wiesenbauer 1976, S.301)
an. (vgl. Wiesenbauer 1976, S.301)
Der Wert der Zahl ![]() findet sich sogar
schon in der Bibel. Im AT im 1. Buch der Könige 7, 23 heißt
es:"Und er machte das Meer, gegossen, von einem Rand zum anderen zehn
Ellen..., und eine Schnur von dreißig Ellen war das Maß ringsherum."
findet sich sogar
schon in der Bibel. Im AT im 1. Buch der Könige 7, 23 heißt
es:"Und er machte das Meer, gegossen, von einem Rand zum anderen zehn
Ellen..., und eine Schnur von dreißig Ellen war das Maß ringsherum."
![]() wird hier also mit dem Wert 3 approximiert.
wird hier also mit dem Wert 3 approximiert.
Im Talmud heißt es: "Was im Umfange drei Handbreiten hat,
ist eine Hand breit." Auch hier wird für ![]() der Wert 3 angenommen. Der Rabbi Nehemiah gab 150 n.Chr. den Wert
für
der Wert 3 angenommen. Der Rabbi Nehemiah gab 150 n.Chr. den Wert
für ![]() mit
mit ![]() an. (vgl. Wiesenbauer 1976, S.301)
an. (vgl. Wiesenbauer 1976, S.301)
Die Priesterhandbücher "Sulba-sûtras" (aus dem
8. Jhdt. v.Chr.) geben die Approximationen 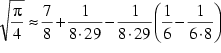 und
und 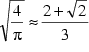 (
( ![]() ist dann
ist dann ![]() ) an, was
) an, was
![]() die Werte
die Werte ![]() 3,088326 bzw.
3,088326 bzw. ![]() 3,088311
zuordnet. (vgl. Ehrenfried Hofmann 1953, S.18f.) Die Erklärung
für letzteren liefert die folgende Vorgehensweise (vgl. Bauer 1928,
S.)
3,088311
zuordnet. (vgl. Ehrenfried Hofmann 1953, S.18f.) Die Erklärung
für letzteren liefert die folgende Vorgehensweise (vgl. Bauer 1928,
S.)
Der Priester Baudhayana (6. Jhdt. v.Chr.) schlägt nämlich einen ganz neuen Weg bei der Umwandlung eines Quadrates in einen flächengleichen Kreis ein.
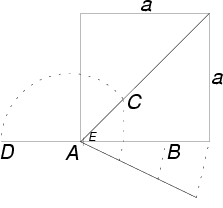
Er verwendet (wahrscheinlich willkürlich) die Summe aus der Seitenlänge
![]() und der Diagonalen
des Quadrates, die den Durchmesser
und der Diagonalen
des Quadrates, die den Durchmesser ![]() des flächengleichen Kreises angeben soll. Diese läßt sich
daher folgendermaßen berechnen:
des flächengleichen Kreises angeben soll. Diese läßt sich
daher folgendermaßen berechnen:
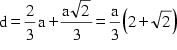
Nebenstehende Skizze zeigt, wie man konstruktiv zur Lösung gelangt.
Da ![]() und
und 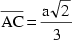 ist
ist ![]() .
. ![]() ist nun der Halbierungspunkt auf
ist nun der Halbierungspunkt auf ![]() , sodaß
, sodaß ![]() den
Radius darstellt.
den
Radius darstellt.
Für den Radius erhält man: ![]()
Einsetzen in die Flächenformel des Kreises und Gleichsetzen mit dem Quadrat ergibt:
![]()
Isoliert man ![]() , so erhält man:
, so erhält man:
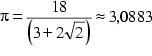
Um 500 v.Chr. waren für ![]() Näherungen
wie zum Beispiel
Näherungen
wie zum Beispiel 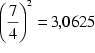 oder noch öfter
oder noch öfter ![]() in Gebrauch, sodaß letzterer Wert oft als "Hinduwert" bezeichnet
wird. (vgl. Mäder 1989, S.51 und Wiesenbauer 1976, S.302)
in Gebrauch, sodaß letzterer Wert oft als "Hinduwert" bezeichnet
wird. (vgl. Mäder 1989, S.51 und Wiesenbauer 1976, S.302)
Daneben fand der "praktische" Wert 3 sehr oft Anwendung.
Antiphon (430 v.Chr.) war der Meinung, daß die Quadratur
des Kreises und damit die exakte Bestimmung von ![]() möglich sein müsse, da sich jedes Polygon in ein Quadrat verwandeln
läßt. Seine Idee ging nämlich davon aus, dem Kreis Vielecke
mit immer größerer Seitenzahl einzuschreiben, sodaß diese
schließlich nicht mehr vom Kreis unterscheidbar sind und damit der
Kreis völlig "erschöpft" ist. Auf Grund dieser Vorgehensweise
nennt man diese Technik "Exhaustions-Methode" (Der
Ausdruck stammt ursprünglich aus dem Griechischen. Der lateinische
Ausdruck heißt "exhaurire", was herausnehmen, erschöpfen,
vollenden bedeutet.). Damit legte Antiphon den Grundstein für
die erfolgreiche Arbeit vieler Mathematiker in späterer Zeit nicht
zuletzt des Archimedes, der eben diese Methode anwandte. (vgl. Bauer
1928, S.6)
möglich sein müsse, da sich jedes Polygon in ein Quadrat verwandeln
läßt. Seine Idee ging nämlich davon aus, dem Kreis Vielecke
mit immer größerer Seitenzahl einzuschreiben, sodaß diese
schließlich nicht mehr vom Kreis unterscheidbar sind und damit der
Kreis völlig "erschöpft" ist. Auf Grund dieser Vorgehensweise
nennt man diese Technik "Exhaustions-Methode" (Der
Ausdruck stammt ursprünglich aus dem Griechischen. Der lateinische
Ausdruck heißt "exhaurire", was herausnehmen, erschöpfen,
vollenden bedeutet.). Damit legte Antiphon den Grundstein für
die erfolgreiche Arbeit vieler Mathematiker in späterer Zeit nicht
zuletzt des Archimedes, der eben diese Methode anwandte. (vgl. Bauer
1928, S.6)
Ein Zeitgenosse Antiphons, Bryson von Herakläa, glaubte, daß die Kreisfläche das arithmetische Mittel aus dem Flächeninhalt des um- und eingeschriebenen Vielecks sei. Obwohl wir heute wissen, daß das nicht korrekt ist, war Brysons Arbeit dennoch wichtig, da er den Begriff einer oberen und unteren Schranke einführte. (vgl. Bauer 1928, S.6)
Seiner Idee lag die Erweiterung der klassischen Konstruktionsmethoden, die sich auf die Verwendung von Zirkel und Lineal beschränkten, durch eine neue Kurve zugrunde, mit der die Quadratur des Kreises schließlich gelungen sein soll. Die "Quadratrix" des Hippias wird mechanisch wie folgt erzeugt:
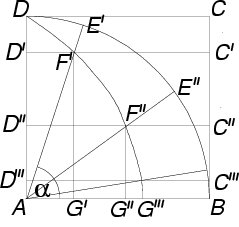
Definition der "Quadratrix": Ein Viertelkreis mit dem
Radius AB dreht sich gleichmäßig im Quadrat ABCD
von D nach B um A. (Die gestrichenen Punkte geben
die sich im Laufe der Bewegung ändernde Position an. C, D,
E, F und G sind solche "wandernde" Punkte,
wobei gleich gestrichene zum selben Zeitpunkt an der jeweiligen Position
sind). Da sich gleichzeitig eine Strecke C´D´ gleichmäßig
von CD aus parallel zu CD nach AB bewegt, bilden die
Schnittpunkte dieser sich nach unten bewegenden Strecke mit dem sich in
Richtung B aufspannenden Bogen den Ort der neuen Kurve. Die Winkelgeschwindigkeit
von ![]() ist dabei proportional
zur Geschwindigkeit, mit der sich C´D´ nach unten bewegt,
sodaß C´D´ die Seite AB erreicht, wenn
ist dabei proportional
zur Geschwindigkeit, mit der sich C´D´ nach unten bewegt,
sodaß C´D´ die Seite AB erreicht, wenn
![]() . Mit
. Mit ![]() ist
ist ![]() gemeint.
gemeint.
Nach Definition gilt: ![]()
Die Bogenlängen verhalten sich folgendermaßen:
![]()
Außerdem existiert die Proportion: ![]() (1)
(1)
Weiters gilt: 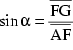
Umformen und erweitern mit ![]() ergibt:
ergibt: 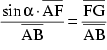
Verwendet man (1) und ersetzt die Quadratseite AB durch a und AF durch s, so ergibt sich:
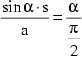
Neuerliches Umformen ergibt: ![]()
Unter der Voraussetzung des Limesbegriffs kann man nun den Grenzübergang
für ![]() gegen 0 durchführen.
gegen 0 durchführen.
![]() (2)
(2)
Der Bogen ![]() ist
ein Viertelkreis. Seine Länge beträgt daher nach der Formel für
den Kreisumfang
ist
ein Viertelkreis. Seine Länge beträgt daher nach der Formel für
den Kreisumfang ![]() , wobei dem Radius r die Seite
, wobei dem Radius r die Seite ![]() entspricht. Folglich beträgt die Länge des Bogens
entspricht. Folglich beträgt die Länge des Bogens ![]() , was entsprechend (2) gleichbedeutend ist mit
, was entsprechend (2) gleichbedeutend ist mit ![]() .
. ![]() ist somit durch
ist somit durch ![]() definiert, wodurch sich auch die Kreisfläche bestimmen läßt.
definiert, wodurch sich auch die Kreisfläche bestimmen läßt.
Konkret wird durch die Strecke ![]() der Radius eines Kreises festgelegt, dessen Umfang genau gleich ist jenem
des Quadrats, in dem die "Quadratrix" konstruiert wurde: Der
Umfang des Quadrats beträgt
der Radius eines Kreises festgelegt, dessen Umfang genau gleich ist jenem
des Quadrats, in dem die "Quadratrix" konstruiert wurde: Der
Umfang des Quadrats beträgt ![]() . Der Umfang des Kreises mit dem Radius
. Der Umfang des Kreises mit dem Radius ![]() beträgt
beträgt ![]() .
Er ist also genau gleich groß wie jener des Quadrats. (vgl. Mainzer
1980, S.34)
.
Er ist also genau gleich groß wie jener des Quadrats. (vgl. Mainzer
1980, S.34)
Er lieferte die erste präzise Definition, daß der Flächeninhalt von Kreisen immer im selben Verhältnis zum Quadrat des Durchmessers steht. Außerdem weckte er die Hoffnung, daß die Quadratur des Kreises mit Zirkel und Lineal in einer endlichen Anzahl von Schritten lösbar sei, da es ihm gelang, verschiedene "Möndchen" zu quadrieren.
Er betrachtete zunächst ein gleichschenkeliges, rechtwinkeliges
Dreieck in einem Halbkreis. Die drei Viertelkreisbögen a, b
und c, die das Möndchen bilden, schließen mit den Katheten
beziehungsweise der Hypotenuse die drei Kreissegmente A, B
und C ein. Hippokrates bewies nun, daß ![]() gilt.
gilt.
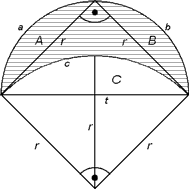
Der Flächeninhalt des Viertelkreissegments C läßt
sich berechnen, indem man vom Flächeninhalt des Viertelkreises jenen
des gleichschenkeligen Dreiecks darunter abzieht.
![]()
Gemäß dem pythagoreischen Lehrsatz gilt zwischen r
und t die Beziehung ![]() . Der Flächeninhalt des Viertelkreissegments C läßt
sich folglich durch die Länge der Sehne t berechnen:
. Der Flächeninhalt des Viertelkreissegments C läßt
sich folglich durch die Länge der Sehne t berechnen:
![]() (1)
(1)
Aus Symmetriegründen ist A natürlich gleich groß wie B, weshalb sich die Summe von A und B gemäß obiger Formel ausdrücken läßt, wobei t natürlich durch die neue Sehne r ersetzt wird:
![]()
Da ![]() gilt, erhält
man weiters:
gilt, erhält
man weiters:
![]()
Da dieser Ausdruck äquivalent zu (1) ist, ist bewiesen, daß
die Summe der Flächeninhalte von A und B gleich jenem
von C ist. Daraus folgt, daß der Flächeninhalt des Möndchens
gleich jenem des gleichschenkeligen, rechtwinkeligen Dreiecks ist: ![]()
Ganz ähnlich lassen sich auch Möndchen "quadrieren", denen ein Trapez zugrunde liegt. (vgl. Mainzer 1980, S.33)
Euklid (ca. 350 v.Chr.) gelang der Beweis, daß ![]() gilt. Doch erst Archimedes konnte rund 100 Jahre später diese Ungleichung
verfeinern.
gilt. Doch erst Archimedes konnte rund 100 Jahre später diese Ungleichung
verfeinern.
(vgl. Bauer 1928, S.6ff.)
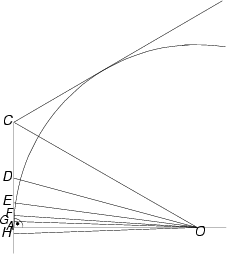
Ausgangspunkt der Berechnungen des Archimedes war der Einheitskreis, dem er regelmäßige 6-Ecke ein- und umbeschrieb. In nebenstehender Skizze erkennt man einen vergrößerten Ausschnitt dieser Konstruktion.
O sei der Mittelpunkt, A der Berührungspunkt einer
Tangente, die eine Seite des umbeschriebenen 6-Ecks bildet. Da ein regelmäßiges
6-Eck aus 6 gleichseitigen Dreiecken besteht und ![]() als Höhe auf AC eines davon halbiert folgt, daß
als Höhe auf AC eines davon halbiert folgt, daß
 .
.
Daraus folgt  (Es ist nicht bekannt, wie Archimedes zu diesem Ergebnis
kommt, er mußte aber schon gewußt haben, daß gilt.)
(Es ist nicht bekannt, wie Archimedes zu diesem Ergebnis
kommt, er mußte aber schon gewußt haben, daß gilt.)
und weiters ![]()
Addition der beiden Proportionen ergibt:
![]() (1)
(1)
Nun verdoppelt man die Seitenzahl zum 12-Eck, indem man ![]() halbiert (stellvertretend für alle 6 Winkel in O). Daraus
ergibt sich der neue Punkt D.
halbiert (stellvertretend für alle 6 Winkel in O). Daraus
ergibt sich der neue Punkt D. ![]() ist daher eine halbe Seite des neuen 12-Ecks. Folglich gilt
ist daher eine halbe Seite des neuen 12-Ecks. Folglich gilt ![]() .
.
Weiters gilt: ![]()
Daraus folgt: ![]()
Und schließlich: ![]()
Nach Vertauschen der Innenglieder erhält man: ![]()
Einsetzen in (1) ergibt: ![]() (2)
(2)
Quadrieren: ![]()
Und "erweitern": ![]() (3)
(3)
![]() ist gemäß
dem pythagoreischen Lehrsatz gleich
ist gemäß
dem pythagoreischen Lehrsatz gleich ![]() , was man in (3) einsetzen kann:
, was man in (3) einsetzen kann:
![]()
Wurzelziehen ergibt: ![]()
Addition mit (2) ergibt: 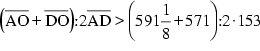 (4)
(4)
Verdoppeln der Seitenzahl zum 24-Eck bedeutet neuerlich ein Halbieren
von ![]() durch die Gerade
OE.
durch die Gerade
OE.
Genauso, wie oben stellt man der Reihe nach folgende Proportionen auf:
![]()
![]()
![]()
Das läßt sich nun in (4) einsetzen: 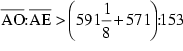
Und ergibt: ![]() (5)
(5)
Wie vorhin "erweitert" man nun:
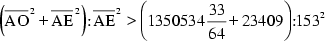
Nun wendet man den Satz von Pythagoras an und radiziert:
![]() (6)
(6)
Mit Halbieren von ![]() beginnt die Prozedur von vorne:
beginnt die Prozedur von vorne:
![]()
![]()
![]()
Wegen (5) und (6) erhält man: ![]() (7)
(7)
Dann: ![]()
![]()
![]() (8)
(8)
Nun halbiert man ![]() und erhält:
und erhält:
![]()
![]()
![]()
Wegen (7) und (8) erhält man nun: ![]() (9)
(9)
In der Skizze erkennt man, daß ![]() , weshalb
, weshalb ![]() ein Achtel
von
ein Achtel
von ![]() sein muß.
Daraus folgt, daß wir das umbeschriebene 96-Eck des Archimedes, dessen
eine Seite also GH ist, nachvollzogen haben.
sein muß.
Daraus folgt, daß wir das umbeschriebene 96-Eck des Archimedes, dessen
eine Seite also GH ist, nachvollzogen haben.
Wenn man (9) erweitert, erhält man:
![]() .
.
![]() ist aber gerade
ist aber gerade
![]() , d.h. eine Seite
des 96-Ecks, folglich ist
, d.h. eine Seite
des 96-Ecks, folglich ist ![]() genau der Umfang
genau der Umfang ![]() des 96-Ecks und darüber hinaus
des 96-Ecks und darüber hinaus ![]() gerade der Durchmesser des Einheitskreises, sodaß man schreiben kann:
gerade der Durchmesser des Einheitskreises, sodaß man schreiben kann:
![]()
Vertauschen der Glieder dreht auch des Ungleichheitszeichen um:
![]()
Da ![]() ist sicherlich
ist sicherlich

Es ist also bewiesen, daß ![]() sein muß.
sein muß.
Die untere Grenze erhält man durch Einschreiben von regelmäßigen Polygonen. Die Skizze verdeutlicht abermals:
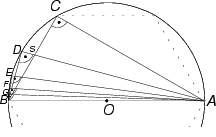
Dem Einheitskreis mit Mittelpunkt O wird ein Sechseck eingeschrieben,
dessen 4 Eckpunkte A, B und C auf dem Halbkreis aufgetragen
sind. Da das Sechseck wieder aus sechs gleichseitigen Dreiecken besteht,
gilt ![]() . Im Thaleskreis
muß
. Im Thaleskreis
muß ![]() ein rechter
Winkel sein, sodaß
ein rechter
Winkel sein, sodaß ![]() und damit
und damit ![]() .
.
Folglich gilt: ![]() (10)
(10)
(Der Ursprung dieser Näherung ist unbekannt, doch Archimedes
wußte offensichtlich schon, daß gilt.)
AD halbiert ![]() und hat mit BC den Schnittpunkt S, sodaß die beiden Dreiecke
ABD und BDS entstehen.
und hat mit BC den Schnittpunkt S, sodaß die beiden Dreiecke
ABD und BDS entstehen. ![]() ist natürlich gleich
ist natürlich gleich ![]() , da AD nach Voraussetzung
, da AD nach Voraussetzung ![]() halbiert,
halbiert, ![]() ist aber
der (gleich große) Normalwinkel zu
ist aber
der (gleich große) Normalwinkel zu ![]() , woraus folgt, daß
, woraus folgt, daß ![]() gleich
gleich ![]() ist. Weiters
haben beide Dreiecke einen rechten Winkel, sodaß sie ähnlich
sein müssen. Daraus lassen sich folgende Proportionen ableiten:
ist. Weiters
haben beide Dreiecke einen rechten Winkel, sodaß sie ähnlich
sein müssen. Daraus lassen sich folgende Proportionen ableiten:
![]()
![]() (11)
(11)
Gemäß dem Strahlensatz gilt: ![]()
Vertauschen der Innenglieder bringt: ![]()
Folglich gilt: ![]() (12)
(12)
Addition von (11) und (12) ergibt ![]()
![]() (13)
(13)
Nach Voraussetzung gilt: ![]()
Addiert man (10) hinzu, so folgt: ![]()
Gemäß (13) gilt daher: ![]() (14)
(14)
Quadrieren und "Erweitern" bewirken:
![]()
Anwendung des Satzes von Pythagoras:
![]()
Und Wurzelziehen: ![]()
Oder vereinfacht angeschrieben: ![]() (15)
(15)
![]() wird nun von
AE halbiert, sodaß sich die Seitenzahl des eingeschriebenen
regelmäßigen Polygons zum 12-Eck verdoppelt. Obigem Schema folgend
erhält man:
wird nun von
AE halbiert, sodaß sich die Seitenzahl des eingeschriebenen
regelmäßigen Polygons zum 12-Eck verdoppelt. Obigem Schema folgend
erhält man:
![]()
Addition von (14) und (15) ergibt: ![]()
Daraus folgt: ![]()
Erweitern der rechten Seite mit ![]() und Zusammenfassen ergibt:
und Zusammenfassen ergibt:
![]() (16)
(16)
Quadrieren und anschließende Anwendung des pythagoreischen Lehrsatzes ergeben:
![]()
![]() (17)
(17)
Neuerlich wird halbiert und durch Verwendung von (16) und (17) gelangt man zu:
![]()
Aus dem Erweitern mit ![]() folgt:
folgt: ![]() (18)
(18)
Quadrieren: ![]()
Und "Erweitern": ![]()
Satz von Pythagoras: ![]()
Und Radizieren: ![]() (19)
(19)
Zuletzt geht man zum 96-Eck über, indem man nochmals halbiert:
Addition von (18) und (19) und übliches Umformen ergeben:
![]()
Quadrieren und die Anwendung des Satzes von Pythagoras führen zu:
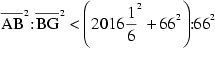
Vereinfachen und Umdrehen der Glieder erzeugt: ![]()
Da ![]() eine Seite
des 96-Ecks ist, kann man folgende Proportion aufstellen:
eine Seite
des 96-Ecks ist, kann man folgende Proportion aufstellen:
![]()
Damit ist bewiesen, daß das Verhältnis ![]() des eingeschriebenen 96-Ecks kleiner ist als
des eingeschriebenen 96-Ecks kleiner ist als ![]() .
.
Führt man dieses Ergebnis nun mit dem Resultat aus dem umgeschriebenen 96-Eck zusammen, so erhält man die berühmte Ungleichung des Archimedes:
![]()
Appollonius von Perga (262-190 v.Chr.) soll den Wert ![]() gefunden haben, welcher später auch immer wieder in Indien auftaucht
und mit jenem des Ptolemäus übereinstimmt. Seine Berechnungsmethode
ist jedoch unbekannt. (vgl. Boyer 1968, S.158)
gefunden haben, welcher später auch immer wieder in Indien auftaucht
und mit jenem des Ptolemäus übereinstimmt. Seine Berechnungsmethode
ist jedoch unbekannt. (vgl. Boyer 1968, S.158)
Heron von Alexandria (um 100 n.Chr.) gelang es angeblich, die
Methode des Archimedes zu verfeinern, sodaß er zur folgenden Approximation
gelangte: ![]() . Es
ist aber nicht vollständig geklärt, ob dieser Ausdruck wirklich
von ihm stammt. (vgl. Ehrenfried Hofmann 1953, S.38)
. Es
ist aber nicht vollständig geklärt, ob dieser Ausdruck wirklich
von ihm stammt. (vgl. Ehrenfried Hofmann 1953, S.38)
Der griechische Astronom Claudius Ptolemäus (2. Jhdt. n.Chr.)
nützte die Vorarbeit des Archimedes und setzte dessen Methode bis
zum 720-Eck fort. Damit erreichte er für ![]() die Näherung
die Näherung ![]() .
.
Hier begnügte man sich lange Zeit mit dem Wert 3 als Approximation
für ![]() , die im "Heiligen Buch
der Rechenkunst" "Chou-pei-suan-ching" festgehalten wurde.
(vgl. Bauer 1928, S.4)
, die im "Heiligen Buch
der Rechenkunst" "Chou-pei-suan-ching" festgehalten wurde.
(vgl. Bauer 1928, S.4)
Liu Hui fand im Jahre 264 n.Chr. mit Hilfe eines 192-Ecks
und der bewährten Methode des Archimedes, daß die Ungleichung
![]() gilt. Als er ein
3072-Eck benützte, approximierte er
gilt. Als er ein
3072-Eck benützte, approximierte er ![]() mit dem Wert 3,14159. (vgl. Wiesenbauer 1976, S.302)
mit dem Wert 3,14159. (vgl. Wiesenbauer 1976, S.302)
Der Astronom Tsu Chu'ung-Chi (430-501) und sein Sohn Tsu Keng-Chi
fanden den Ausdruck ![]() und die Näherung
und die Näherung ![]() , die immerhin 6 richtige Nachkommastellen aufweist und der "beste"
Bruch ist, dessen Faktoren kleiner als
, die immerhin 6 richtige Nachkommastellen aufweist und der "beste"
Bruch ist, dessen Faktoren kleiner als ![]() sind. Über den Ursprung des recht einfachen Bruches gibt es nur Vermutungen,
die besagen, daß Tsu einfach die bekannten Brüche von Ptolemäus
und Archimedes verwendet hat und die Differenz der Zähler und Nenner
bildete:
sind. Über den Ursprung des recht einfachen Bruches gibt es nur Vermutungen,
die besagen, daß Tsu einfach die bekannten Brüche von Ptolemäus
und Archimedes verwendet hat und die Differenz der Zähler und Nenner
bildete: ![]() (vgl.
Wells 1991, S.49)
(vgl.
Wells 1991, S.49)
Auch der indische Mathematiker Brahmagupta (geboren 598 n.Chr.)
fand den Wert ![]() ,
indem er die Summe der Seitenlängen von 12-, 24-, 48- und 96-seitigen
Polygonen, die er einem Kreis mit dem Durchmesser 10 E einschrieb,
berechnete. Diese ergeben
,
indem er die Summe der Seitenlängen von 12-, 24-, 48- und 96-seitigen
Polygonen, die er einem Kreis mit dem Durchmesser 10 E einschrieb,
berechnete. Diese ergeben ![]() und
und ![]() . Weiters nahm
er an, daß dies schließlich zu
. Weiters nahm
er an, daß dies schließlich zu ![]() , dem Kreisumfang, führen würde. Für
, dem Kreisumfang, führen würde. Für ![]() ergäbe sich dann der Wert
ergäbe sich dann der Wert 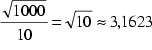 (vgl. Castellanos 1988, S.68 )
(vgl. Castellanos 1988, S.68 )
Um 510 n.Chr. gab Aryabhatiya folgende Regel zur Bestimmung von
![]() an: "Addiere 4 zu 100, multipliziere
mit 8, und addiere 62 000. Das Resultat ist der ungefähre Wert
des Umfanges eines Kreises mit dem Durchmesser 20 000." (vgl.
Kaiser 1984, S.146)
an: "Addiere 4 zu 100, multipliziere
mit 8, und addiere 62 000. Das Resultat ist der ungefähre Wert
des Umfanges eines Kreises mit dem Durchmesser 20 000." (vgl.
Kaiser 1984, S.146) ![]() wird also mit
wird also mit
![]() approximiert, einem
Wert, der auch im Paulisha Siddhanta aufscheint und mit jenem des Ptolemäus
(siehe Seite
approximiert, einem
Wert, der auch im Paulisha Siddhanta aufscheint und mit jenem des Ptolemäus
(siehe Seite ![]() )
übereinstimmt. Bei Aryabhatiya findet man auch eine Aufgabe, die einem
Kreis mit dem Radius 3438 E einen Umfang von 21600 E zuordnet,
was für
)
übereinstimmt. Bei Aryabhatiya findet man auch eine Aufgabe, die einem
Kreis mit dem Radius 3438 E einen Umfang von 21600 E zuordnet,
was für ![]() den Wert
den Wert ![]() 3,14136 bedeutet. Im "Bahmasphuta Siddhanta" wird der Radius
bei identischem Umfang mit 3270 E angegeben, was für
3,14136 bedeutet. Im "Bahmasphuta Siddhanta" wird der Radius
bei identischem Umfang mit 3270 E angegeben, was für ![]() ergibt. (vgl. Boyer 1968, S.241) Schließlich verwendet auch
Bhaskara um 1150 diesen Wert als einen exakten für
ergibt. (vgl. Boyer 1968, S.241) Schließlich verwendet auch
Bhaskara um 1150 diesen Wert als einen exakten für ![]() , während er den Bruch
, während er den Bruch ![]() , den Archimedes als erster berechnete, als grobe Näherung angibt.
, den Archimedes als erster berechnete, als grobe Näherung angibt.
Ibn Alhaitam (958-1038) behandelte selbständig die Quadratur des Kreises. (vgl. Bauer 1928, S.13f.)
Dem Perser Jemshid Al-Kashi gelang es um 1430 n.Chr. sechzehn
Dezimalstellen von ![]() korrekt zu berechnen.
(vgl. Wiesenbauer 1976, S.302)
korrekt zu berechnen.
(vgl. Wiesenbauer 1976, S.302)
Den Arabern verdanken wir aber in erster Linie die Überlieferung der Ergebnisse von griechischen und indischen Mathematikern.
Leonardo von Pisa (1170-1240?), genannt Fibonacci, gelang
es lediglich drei korrekte Dezimalstellen von ![]() zu ermitteln.
zu ermitteln.
(vgl. Pech 1989, S.10f.) Dieser Kardinal und zu seiner Zeit bedeutende
Gelehrte wird in der Literatur oft mit seinem latinisierten Namen Cusanus
erwähnt. Anfangs betrachtete er 3,1423 als den exakten Wert von ![]() , doch die folgende Methode erlaubte ihm,
, doch die folgende Methode erlaubte ihm, ![]() beliebig genau zu approximieren.
beliebig genau zu approximieren.
Einem Kreis wird ein regelmäßiges n-Eck eingeschrieben, sodaß dessen Umfang 1 ist.
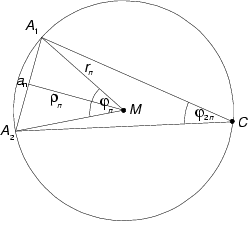
Aus nebenstehender Skizze ersieht man: ![]() bezeichnet den Inkreisradius,
bezeichnet den Inkreisradius, ![]() den Umkreisradius,
den Umkreisradius, ![]() die Seitenlänge des regelmäßigen n-Ecks (wobei nach Voraussetzung
gilt:
die Seitenlänge des regelmäßigen n-Ecks (wobei nach Voraussetzung
gilt: ![]() ), M
den Mittelpunkt des Umkreises und
), M
den Mittelpunkt des Umkreises und ![]() den Zentriwinkel A1MA2 des n-Ecks, der sich durch
den Zentriwinkel A1MA2 des n-Ecks, der sich durch ![]() berechnen läßt.
berechnen läßt.
Gemäß dem Peripheriewinkelsatz gilt: ![]() (1)
(1)
![]() ist also der
Zentriwinkel des 2n-Ecks, womit der Schritt vom n-Eck zum 2n-Eck vollzogen
wäre. Im 2n-Eck gilt aber noch immer, daß
ist also der
Zentriwinkel des 2n-Ecks, womit der Schritt vom n-Eck zum 2n-Eck vollzogen
wäre. Im 2n-Eck gilt aber noch immer, daß ![]() , weshalb der Umfang nun 2 wäre. Um den Umfang wieder auf 1 zu reduzieren,
muß man
, weshalb der Umfang nun 2 wäre. Um den Umfang wieder auf 1 zu reduzieren,
muß man ![]() im
Verhältnis 2:1 verkleinern.
im
Verhältnis 2:1 verkleinern.
Folglich ergibt sich: ![]() (2)
(2)
In ![]() gilt auf
Grund des pythagoreischen Lehrsatzes:
gilt auf
Grund des pythagoreischen Lehrsatzes:
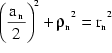 (3)
(3)
In ![]() gilt aus
demselben Grund:
gilt aus
demselben Grund: 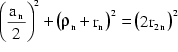 (4)
(4)
![]() kann man sich
nun durch (3) ausdrücken, in (4) einsetzen:
kann man sich
nun durch (3) ausdrücken, in (4) einsetzen:
![]()
Und ausmultiplizieren: ![]()
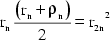 ist entsprechend
(2) gleichbedeutend mit
ist entsprechend
(2) gleichbedeutend mit ![]()
Schließlich erhält man: ![]() . Die zweite Folge (2) lautet:
. Die zweite Folge (2) lautet: ![]()
Somit haben wir zwei gekoppelte rekursive Folgen erhalten, in die man beispielsweise die Werte für ein Quadrat einsetzen kann. Auf diese Weise erhalten wir die beiden Folgen:
![]()
![]()
Beide Folgen konvergieren gegen 0,159115..., was einen Näherungswert
für ![]() darstellt,
da der Inkreis- und Umkreisradius des n-Ecks jenem des Kreises immer näher
kommen. Da nach Voraussetzung
darstellt,
da der Inkreis- und Umkreisradius des n-Ecks jenem des Kreises immer näher
kommen. Da nach Voraussetzung ![]() ist, ergibt sich für den Radius
ist, ergibt sich für den Radius ![]() , ein Wert der von den obenstehenden Folgen beliebig genau angenähert
wird.
, ein Wert der von den obenstehenden Folgen beliebig genau angenähert
wird.
Adriaen Metius entdeckte zufällig die Näherung ![]() , als er das arithmetische Mittel von Zähler und Nenner der beiden
Näherungen
, als er das arithmetische Mittel von Zähler und Nenner der beiden
Näherungen ![]() und
und ![]() , die auf Berechnungen
seines Vaters beruhten, bildete. Diesen Wert hatte aber schon mehr als
1000 Jahre vor ihm Tsu Ch'ung-Chi gefunden.
, die auf Berechnungen
seines Vaters beruhten, bildete. Diesen Wert hatte aber schon mehr als
1000 Jahre vor ihm Tsu Ch'ung-Chi gefunden.
Der deutsche Astronom Georg Joachim von Lauchen, genannt Rhäticus
(1514-1576), da er in Rätien, dem heutigen schweizer Kanton Graubünden
geboren war, erstellte fünfzehnstellige Tafeln von trigonometrischen
Funktionen, durch die erstaunlich genaue Werte für ![]() berechnet werden können.
berechnet werden können.
Wie bei Eulers Berechnungsmethode noch gezeigt wird gilt, daß
![]() , d.h.
, d.h. ![]() für sehr kleine
für sehr kleine ![]() . Da ein Halbkreis
einen Winkel von
. Da ein Halbkreis
einen Winkel von ![]() überstreicht, kann man den von Rhäticus für
überstreicht, kann man den von Rhäticus für ![]() angegebenen Wert 0,000048481368092 mit 64 800 multiplizieren und erhält
sodann 3,1415926523, was auf 8 Dezimalstellen mit dem tatsächlichen
Wert übereinstimmt. (vgl. Castellanos 1988, S.68)
angegebenen Wert 0,000048481368092 mit 64 800 multiplizieren und erhält
sodann 3,1415926523, was auf 8 Dezimalstellen mit dem tatsächlichen
Wert übereinstimmt. (vgl. Castellanos 1988, S.68)
Tycho de Brahe (1546-1601), ein dänischer Astronom, nahm
für ![]() den Wert
den Wert ![]() an.
an.
Im Jahre 1592 stellte François Viète, lateinisch Vieta genannt, der "Vater" der modernen Algebra, erstmals eine geschlossene Formel vor, die sich leicht aus einem unendlichen Produkt, das Leonard Euler (siehe dort) rund 150 Jahre später fand, ableiten läßt.
1673 fand G.W. Leibniz die einfache, aber nur sehr langsam konvergierende
Formel ![]() , die sich
mit Hilfe der Potenzreihe des Arcustangens ableiten läßt.
, die sich
mit Hilfe der Potenzreihe des Arcustangens ableiten läßt.
Um die Potenzreihe von ![]() zu bilden differenziert man zuerst
zu bilden differenziert man zuerst ![]() implizit:
implizit:
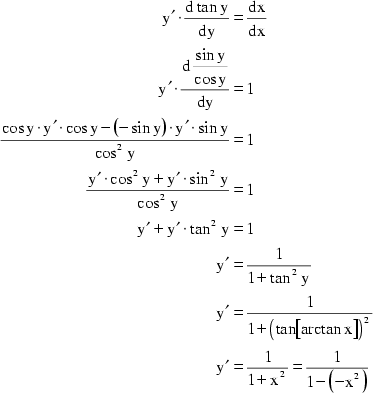
y' läßt sich nun gemäß der Formel für
unendliche geometrische Reihen ![]() in eine Potenzreihe verwandeln. q ist dann
in eine Potenzreihe verwandeln. q ist dann ![]() , sodaß sich folgende Potenzreihe ergibt:
, sodaß sich folgende Potenzreihe ergibt:
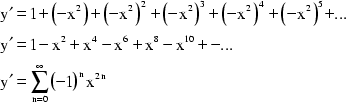
Integriert man diesen Ausdruck gliedweise, so ergibt sich:
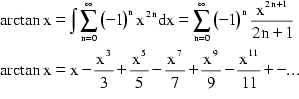
Setzt man nun ![]() , so erhält man wegen
, so erhält man wegen ![]() Leibniz' Ausdruck:
Leibniz' Ausdruck:
![]()
Um die schlechte Konvergenzgeschwindigkeit zu erhöhen, kann man
kleinere Werte für x einsetzen, sodaß man beispielsweise
aus ![]() die schon um
einiges schneller konvergierende Reihe
die schon um
einiges schneller konvergierende Reihe
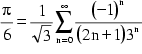
erhält.
Er fand den Ausdruck ![]() , der sich wie folgt ableiten läßt. (vgl. Möwald 1993,
S.117f.)
, der sich wie folgt ableiten läßt. (vgl. Möwald 1993,
S.117f.)
Zuerst betrachtet man das Integral ![]() , wobei
, wobei ![]() ist.
ist. ![]() kann man nun durch
kann man nun durch ![]() ersetzen und partiell integrieren:
ersetzen und partiell integrieren:
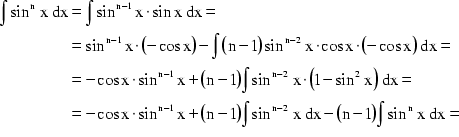
Da auf der rechten Seite noch einmal der Term ![]() auftritt, kann man ihn auf die linke Seite bringen und anschließend
den ganzen Ausdruck vereinfachen:
auftritt, kann man ihn auf die linke Seite bringen und anschließend
den ganzen Ausdruck vereinfachen:
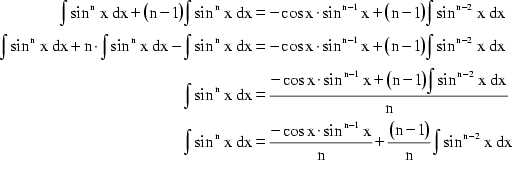
Diese Rekursionsformel bildet Wallis' Grundlage der Approximation von
![]() .
.
Weiters bezieht er sich auf folgende Beziehung, die für ![]() und
und ![]() gültig
ist:
gültig
ist: ![]() (1)
(1)
Sie läßt sich damit begründen, daß alle Funktionswerte der Sinus-Funktion im Intervall [0;1] liegen und daher zu einer positiven Potenz erhoben kleiner werden. Je größer diese Potenz ist, umso kleiner wird daher auch der potenzierte Funktionswert, woraus sich obenstehende Ungleichung ergibt.
Setzt man nun die Grenzen der Integration mit 0 und ![]() fest, so kann man folgendermaßen umformen:
fest, so kann man folgendermaßen umformen:
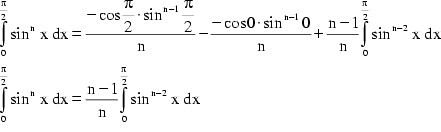
Zuerst setzt man gemäß (1) ![]() , sodaß man vereinfachen kann:
, sodaß man vereinfachen kann:
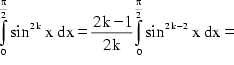
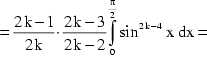
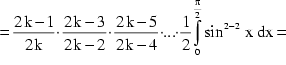
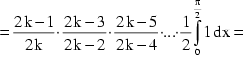
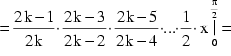
Schließlich erhält man folgendes unendliches Produkt:
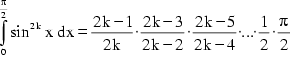
Setzt man gemäß (1) nun ![]() , so kann man wieder vereinfachen:
, so kann man wieder vereinfachen:
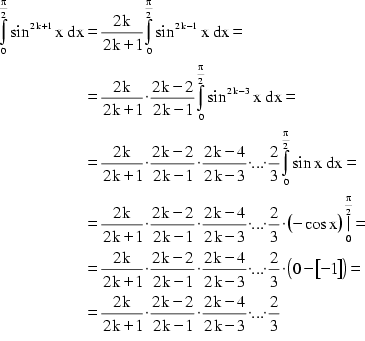 (3)
(3)
Schließlich setzt man (2) und (3) in (1) ein und erhält:
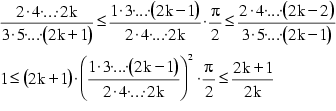 (4)
(4)
Beim Grenzübergang von k nach ![]() wird der rechte Term 1, da
wird der rechte Term 1, da
![]()
ist.
Für (4) ergibt sich somit:
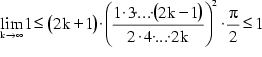
Das bedeutet weiters, daß der Ausdruck in der Mitte gegen 1 strebt:
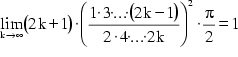
Isoliert man ![]() , so erhält man
die Produktdarstellung von Wallis:
, so erhält man
die Produktdarstellung von Wallis:
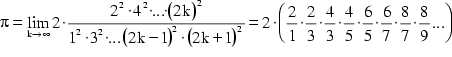
Ein erbitterter Gegner von Wallis' war der englische Philosoph Thomas Hobbes (1588-1679), der sich 25 Jahre lang mit Wallis vornehmlich in Form von Briefen bekriegte, in denen sie ihre neuesten Theorien und Berechnungen festhielten und versuchten, diejenigen des "Gegners" zu widerlegen.
Um 1700 herum war Jacob Marcelis der Meinung, daß es ihm gelungen
sei, den Kreis zu quadrieren, und damit den exakten Wert für ![]() zu bestimmen. Diesen gab er mit
zu bestimmen. Diesen gab er mit ![]() an. (vgl. Wells 1990, S.52)
an. (vgl. Wells 1990, S.52)
1706 gelang John Machin ein Geniestreich: Auf Grund der folgenden sehr effektiven Berechnungsmethode konnte er 100 korrekte Dezimalstellen erzielen. (vgl. Peitgen 1992, S.177)
Eine weitere Möglichkeit, die Konvergenz der Arcustangens-Reihen
zu verbessern, besteht nämlich darin, unter Verwendung des Additionstheorems
![]() folgendermaßen
vorzugehen:
folgendermaßen
vorzugehen:
Setzt man willkürlich ![]() , so berechnet man leicht nach obiger Beziehung
, so berechnet man leicht nach obiger Beziehung
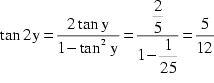
und weiters
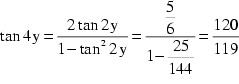 (1)
(1)
Außerdem erhält man unter Berücksichtigung von ![]()
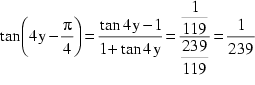
aus selbiger Beziehung.
Unter Anwendung des Arcustangens erhält man daraus:
![]()
Schließlich gelangt man mit Hilfe von (1) zu:
![]()
Dieser Ausdruck stellt bereits eine sehr effiziente Berechnungsmethode
dar, wenn man dabei die Potenzreihe des Arcustangens (siehe Seite ![]() ) benützt.
) benützt.
Erst 1958 entdeckte G.F. FREEMAN (Math. Gazette 42, S.285) folgende noch schneller konvergierende Formel (zitiert nach Koecher 1987, S.162)
![]()
Genauso gut eignet sich auch die Potenzreihe (Taylor-Reihe) des Arcussinus
zur Approximation von ![]() : (vgl. Bronstejn
u.a. 1991, S.372)
: (vgl. Bronstejn
u.a. 1991, S.372)
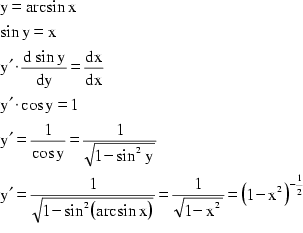
Letzterer Ausdruck läßt sich nun gemäß dem binomischen Lehrsatz
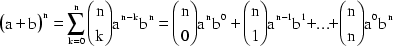
in die folgende unendliche Potenzreihe verwandeln:
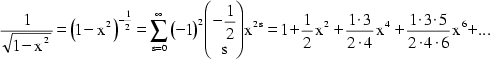
Durch gliedweises Integrieren gelangt man zu:
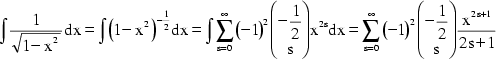
Man erhält schließlich:
![]()
Nun kann man wieder beliebige Werte für x einsetzen und
erhält so entsprechende Reihen zur Approximation von ![]() . Für
. Für ![]() ergibt
sich:
ergibt
sich:
![]()
Euler war der erste, der für das Verhältnis des Umfangs zum
Durchmesser eines Kreises den griechischen Buchstaben für p, nämlich
![]() , verwendete. Der Grund für diese
Bezeichnung dürfte sein, daß der Umkreis griechisch "periphereia"
heißt und der Umfang des Einheitskreises genau
, verwendete. Der Grund für diese
Bezeichnung dürfte sein, daß der Umkreis griechisch "periphereia"
heißt und der Umfang des Einheitskreises genau ![]() ist. (KAISER gibt für die "Erfinder"
des Symbols
ist. (KAISER gibt für die "Erfinder"
des Symbols ![]() zwei englische Mathematiker
namens William Oughtred und Issac Barrow an, die den Umfang des Kreises
mit
zwei englische Mathematiker
namens William Oughtred und Issac Barrow an, die den Umfang des Kreises
mit ![]() bezeichneten. Erst der Schriftsteller
William Jones soll 1706
bezeichneten. Erst der Schriftsteller
William Jones soll 1706 ![]() als Symbol
in unserem heutigen Sinn verwendet haben.)
als Symbol
in unserem heutigen Sinn verwendet haben.)
Euler fand die Beziehung ![]() , die eine Voraussetzung für Lindemanns Beweis der Transzendenz von
, die eine Voraussetzung für Lindemanns Beweis der Transzendenz von
![]() ist. Auch die folgende stammt von ihm:
ist. Auch die folgende stammt von ihm:
![]() und ein unendliches
Produkt, in dem nur Primzahlen auftreten: (vgl. Wells 1990, S. 54)
und ein unendliches
Produkt, in dem nur Primzahlen auftreten: (vgl. Wells 1990, S. 54)
![]()
Darüber hinaus fand er auch die Beziehung ![]() , mit der sich
, mit der sich ![]() approximieren läßt,
und durch die man bei der im folgenden ausgeführten Vereinfachung
zu Vietas Produktdarstellung von
approximieren läßt,
und durch die man bei der im folgenden ausgeführten Vereinfachung
zu Vietas Produktdarstellung von ![]() gelangt.
gelangt.
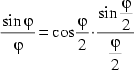 (1)
(1)
denn (vgl. Bronstejn 1991, S.182):
![]() (2)
(2)
Das heißt: 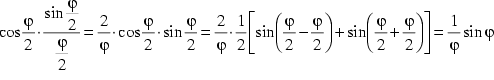
entsprechend (1) gilt weiter: 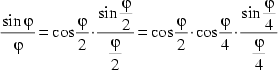 , was sich wieder mit (2) beweisen läßt. Da sich diese Umformung
beliebig fortsetzen läßt, erhält man schließlich
einen Ausdruck von der Form:
, was sich wieder mit (2) beweisen läßt. Da sich diese Umformung
beliebig fortsetzen läßt, erhält man schließlich
einen Ausdruck von der Form:
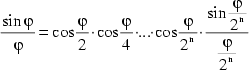 (3)
(3)
Der Term ![]() konvergiert
gegen 1, sodaß man zuletzt aus (3) Eulers Ausdruck erhält:
konvergiert
gegen 1, sodaß man zuletzt aus (3) Eulers Ausdruck erhält: ![]() (4)
(4)
(vgl. Castellanos 1988, S. 68ff.)
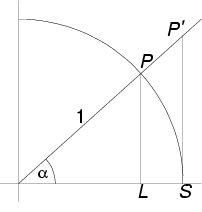
Die Konvergenz des Ausdrucks ![]() läßt sich folgendermaßen beweisen:
läßt sich folgendermaßen beweisen:
Wie in der Skizze erkennbar gilt folgende Ungleichung:
![]()
Die Bogenlänge kann man durch den Winkel im Bogenmaß, und die beiden Strecken durch die entsprechenden Winkelfunktionen im Einheitskreis angeben:
![]()
![]() für
für ![]()
Das ist äquivalent: ![]()
Division durch ![]() ergibt:
ergibt: ![]()
Nun läßt man ![]() gehen und erhält
gehen und erhält ![]()
Da ![]() kann man
vereinfachen:
kann man
vereinfachen: ![]()
![]() ist somit bewiesen.
Da
ist somit bewiesen.
Da ![]() ist, bedeutet
das weiters, daß
ist, bedeutet
das weiters, daß 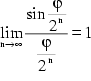 sein muß.
sein muß.
Setzt man nun in (4) ![]() , so erhält man
, so erhält man ![]() (5)
(5)
Gemäß der Beziehung 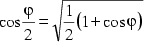 kann man den Ausdruck umformen:
kann man den Ausdruck umformen:
Da ![]() gilt:
gilt: 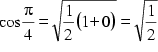
Weiters 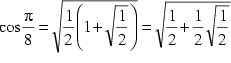
Und auch: 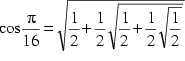
Ersetzt man die entsprechenden Terme in (5), so erhält man den Ausdruck, den schon François Viète im Jahre 1593 fand:
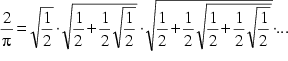
Die Konvergenz dieses Ausdrucks konnte aber erst F. Rudio im Jahre 1891 beweisen.
Im 16. Jahrhundert berechnete Ludolph van Ceulen (1540-1610)
zuerst 15, dann 20, später 32 und schließlich sogar 35 Dezimalstellen
mit Hilfe der Methode des Archimedes, die er auf ein ![]() -Eck, ein
-Eck, ein ![]() -Eck
bzw. ein
-Eck
bzw. ein ![]() -Eck anwandte.
Sein Werk wurde gleich zweifach gewürdigt: Erstens ließ seine
Witwe das Ergebnis seiner Berechnungen in den Grabstein ihres Gatten einmeißeln,
und zweitens erhielt
-Eck anwandte.
Sein Werk wurde gleich zweifach gewürdigt: Erstens ließ seine
Witwe das Ergebnis seiner Berechnungen in den Grabstein ihres Gatten einmeißeln,
und zweitens erhielt ![]() die Bezeichnung
"Ludolph'sche Zahl". (vgl. Ehrenfried Hofmann 1953, S.129)
die Bezeichnung
"Ludolph'sche Zahl". (vgl. Ehrenfried Hofmann 1953, S.129)
Der Niederländer van Roomen errechnete um 1600 auf der Grundlage
eines ![]() -Ecks fünfzehn
Dezimalstellen von
-Ecks fünfzehn
Dezimalstellen von ![]() .
.
Snell(ius) und Huygens verfeinerten schon bekannte Verfahren
vor allem mit Hilfe der weiterentwickelten Trigonometrie. 1621 fand Snellius
durch eine Kombination von ein- und umbeschriebenen regelmäßigen
Vielecken den Ausdruck ![]() , in den man für t einen beliebigen Winkel, der sich durch
, in den man für t einen beliebigen Winkel, der sich durch
![]() ausdrücken läßt, einsetzen
kann, sodaß man durch eine entsprechend genaue Berechnung der Winkelfunktionen
beliebig enge Grenzen für
ausdrücken läßt, einsetzen
kann, sodaß man durch eine entsprechend genaue Berechnung der Winkelfunktionen
beliebig enge Grenzen für ![]() finden
kann. (vgl. Ehrenfried Hofmann 1953, S.129)
finden
kann. (vgl. Ehrenfried Hofmann 1953, S.129)
Newton gelang es 1666 die ersten 16 Stellen von ![]() zu berechnen, indem er die ersten 20 Summanden in
zu berechnen, indem er die ersten 20 Summanden in
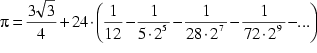
berücksichtigte.
Johann Heinrich Lambert gelang es im Jahre 1761, die Irrationalität
von ![]() zu beweisen. (vgl. Boyer 1968,
S.505)
zu beweisen. (vgl. Boyer 1968,
S.505)
Zuerst zeigte er, daß ![]() nicht rational sein kann, wenn
nicht rational sein kann, wenn ![]() ist. Daraus folgerte er, daß
ist. Daraus folgerte er, daß ![]() nicht rational sein kann, wenn
nicht rational sein kann, wenn ![]() rational ist, wie dies in dem Ausdruck
rational ist, wie dies in dem Ausdruck ![]() der Fall ist. Nach dem Beweis dieses Ausdrucks schloß Lambert, daß
der Fall ist. Nach dem Beweis dieses Ausdrucks schloß Lambert, daß
![]() und damit auch
und damit auch
![]() nicht rational sein können.
nicht rational sein können.
Mit Hilfe von Kettenbrüchen konnte er auch die besten Approximationen
in Form von Brüchen berechnen. Dazu zählen beispielsweise ![]() oder noch genauer
oder noch genauer ![]()
Johann Dase (1824-1861), der als Rechengenie bekannt war, berechnete
in weniger als zwei Monaten 200 Dezimalstellen von ![]() . Auf Empfehlung von C.F. Gauß fand er später eine Anstellung,
bei der er Tafeln für Logarithmen- und Hyperbelfunktionen berechnete.
. Auf Empfehlung von C.F. Gauß fand er später eine Anstellung,
bei der er Tafeln für Logarithmen- und Hyperbelfunktionen berechnete.
Im Jahre 1853 fand William Shanks mit der selben Formel, wie
Machin sie benützt hatte, 707 Stellen der Dezimalbruchentwicklung
von ![]() . Später fand man aber heraus,
daß er sich ab der 528. Stelle verrechnet hatte. Shanks widmete sich
aber auch der hochgenauen Berechnung von Logarithmen, von denen er bis
zu 137 Dezimalstellen fand, und er bestimmte den Wert von
. Später fand man aber heraus,
daß er sich ab der 528. Stelle verrechnet hatte. Shanks widmete sich
aber auch der hochgenauen Berechnung von Logarithmen, von denen er bis
zu 137 Dezimalstellen fand, und er bestimmte den Wert von ![]() .
.
In jener Zeit wurde erstmals auch die Ziffernfolge von ![]() genauer untersucht. Dabei fiel Auguste de Morgan auf, daß
die Ziffer 7 nur 44 mal im Gegensatz zum erwarteten Mittelwert von etwa
71 mal in Shanks' für
genauer untersucht. Dabei fiel Auguste de Morgan auf, daß
die Ziffer 7 nur 44 mal im Gegensatz zum erwarteten Mittelwert von etwa
71 mal in Shanks' für ![]() errechnetem
Wert auftrat, was an dessen Rechenfehler lag. (vgl. Wells 1990, S. 51)
errechnetem
Wert auftrat, was an dessen Rechenfehler lag. (vgl. Wells 1990, S. 51)
1882 zeigte Lindemann (1852-1939) mit seinem Beweis der Transzendenz
von ![]() , daß
, daß ![]() keine Lösung einer algebraischen Gleichung, das heißt einer
Gleichung mit reellen Koeffizienten und einer endlichen Anzahl von Gliedern
ist. (vgl. Boyer 1968, S.603)
keine Lösung einer algebraischen Gleichung, das heißt einer
Gleichung mit reellen Koeffizienten und einer endlichen Anzahl von Gliedern
ist. (vgl. Boyer 1968, S.603)
Den folgenden nur skizzierten Beweis veröffentlichte er in dem
Artikel "Über die Zahl ![]() "
in den "Mathematischen Annalen" in München.
"
in den "Mathematischen Annalen" in München.
Zuerst bewies Lindemann, daß die Lösung von ![]() nicht algebraisch sein kann. Er wußte aber, daß
nicht algebraisch sein kann. Er wußte aber, daß ![]() dieser Gleichung genügte (das hatte schon Newton bewiesen), woraus
er folgerte, daß
dieser Gleichung genügte (das hatte schon Newton bewiesen), woraus
er folgerte, daß ![]() keine algebraische
Zahl sein kann.
keine algebraische
Zahl sein kann.
1945 wies Ferguson den oben schon erwähnten Fehler in Shanks'
Berechnungen mit Hilfe eines "Tischrechners" nach. Die Nachkriegszeit
wurde also auch zum Computerzeitalter, das die immer genauere Berechnung
von ![]() ermöglichte.
ermöglichte.
Vier Jahre später rechnete ENIAC neunzig Stunden lang an
den ersten 2037 Stellen von ![]() ohne dabei
einen Fehler zu machen.
ohne dabei
einen Fehler zu machen.
Am 29. Juli 1961 wurden auf einer IBM 7090 in New York 100 265
Dezimalstellen von ![]() berechnet. Die Rechenzeit
betrug nur noch 8 Stunden.
berechnet. Die Rechenzeit
betrug nur noch 8 Stunden.
1967 berechnete der französische Computer CDC 6600 nicht
weniger als 500 000 Stellen von ![]() .
.
1988 waren es bereits ![]() Stellen, die Yoshiaki Tamura und Tasumasa Kanada mit einem
Computer berechneten. (vgl. Wells 1990, S.54f.)
Stellen, die Yoshiaki Tamura und Tasumasa Kanada mit einem
Computer berechneten. (vgl. Wells 1990, S.54f.)
Ihrem Algorithmus liegen Untersuchungen von Gauß zum arithmetischen und geometrischen Mittel zugrunde, was sie schließlich zu folgender Schleife führte:
Die Startwerte sind:
Durchläuft man die Schritte 1 bis 5 nacheinander, so ergibt sich
nach jedem Durchlauf die immer bessere Approximation 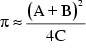 .
.
1986 berechnete Kanada 133,5 Millionen Stellen. Zur Erstellung des neuen Programms benötigte er rund 8 Monate, der Computer arbeitete 37 Stunden lang und druckte das Ergebnis auf 20 000 Blatt Papier aus.
Unter dieser Bezeichnung werden alle Verfahren zusammengefaßt, die sich der Wahrscheinlichkeitsrechnung und Statistik bedienen, um einen Sachverhalt mit einer großen Anzahl von Versuchen bei einem Zufallsexperiment (daher die Bezeichnung mit dem Namen des Casinoparadieses) nachzuweisen.
(vgl. Kranzer 1989, S.196 und Mäder 1989, S.54f.)
Der Biologe George Louis Leclerc, Comte de Buffon, (1707-1788) warf im
Jahre 1777 ein Problem auf, mit dem sich ![]() rein statistisch approximieren läßt.
rein statistisch approximieren läßt.
Bei diesem Zufallsexperiment wird eine Nadel auf eine Schar paralleler Linien geworfen, deren Normalabstand genau die Länge der Nadel beträgt. Nun stellt sich die Frage, wie groß die Wahrscheinlichkeit ist, daß die Nadel eine der Geraden berührt oder schneidet.
Hat man n-mal geworfen und m-mal das Querliegen registriert,
so kommt der Quotient ![]() dem Wert von
dem Wert von ![]() umso
näher, je größer die Anzahl n der Versuche ist.
Das heißt, daß
umso
näher, je größer die Anzahl n der Versuche ist.
Das heißt, daß ![]() gegen
gegen ![]() strebt.
strebt.
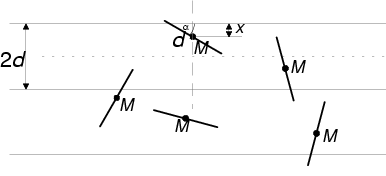
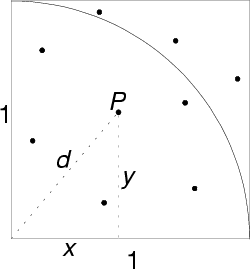
Wie in nebenstehender Skizze erkennbar, sind drei der Geraden eingezeichnet
und mehrere Nadeln, von denen die oberste stellvertretend für alle
übrigen beschriftet ist. M bezeichnet den Mittelpunkt der Nadel,
d die halbe Nadellänge, x die Entfernung der näheren
Geraden von M (die weiter entfernte Gerade kann aus Symmetriegründen
vernachlässigt werden) und 2d die Entfernung von zwei parallelen
Geraden, die definitionsgemäß doppelt so groß wie die
halbe Nadellänge d ist. ![]() bezeichnet jenen Winkel, der von der Nadel und der Geraden eingeschlossen
wird.
bezeichnet jenen Winkel, der von der Nadel und der Geraden eingeschlossen
wird.
Alle möglichen Lagen der Nadel lassen sich somit durch zwei Ungleichungen darstellen:
![]() und
und ![]() ,
,
wobei ![]() , was gleichbedeutend
ist mit
, was gleichbedeutend
ist mit ![]() . Das bedeutet,
daß x auch kleiner sein kann, was der Fall ist, wenn die Nadel
eine Gerade schneidet und nicht nur berührt.
. Das bedeutet,
daß x auch kleiner sein kann, was der Fall ist, wenn die Nadel
eine Gerade schneidet und nicht nur berührt.
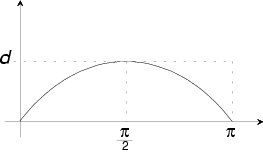
Da die beiden Parameter ![]() und x
in letztgenannter Beziehung stehen, lassen sie sich in einem Koordinatensystem
darstellen, wie es nebenstehend abgebildet ist. Die gesuchte Wahrscheinlichkeit
läßt sich nun durch den Quotienten des Flächeninhalts des
Rechtecks, der alle möglichen Lagen der Nadel bezeichnet, und der
Fläche unter der Sinus-Kurve, die die "günstigen" Lagen,
bei denen die Nadel eine Gerade schneidet, bezeichnet, berechnen:
und x
in letztgenannter Beziehung stehen, lassen sie sich in einem Koordinatensystem
darstellen, wie es nebenstehend abgebildet ist. Die gesuchte Wahrscheinlichkeit
läßt sich nun durch den Quotienten des Flächeninhalts des
Rechtecks, der alle möglichen Lagen der Nadel bezeichnet, und der
Fläche unter der Sinus-Kurve, die die "günstigen" Lagen,
bei denen die Nadel eine Gerade schneidet, bezeichnet, berechnen:
Der Flächeninhalt des Rechtecks ist ![]() .
.
Jener unter der Sinus-Kurve errechnet sich aus:
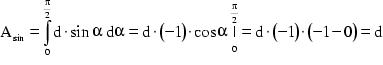
Der Quotient ![]() läßt sich daher vereinfacht anschreiben:
läßt sich daher vereinfacht anschreiben:
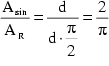 .
.
Damit ist bewiesen, daß die Wahrscheinlichkeit, daß die
Nadel eine Gerade berührt oder schneidet ![]() ist.
ist.
Der Italiener Lazzerini warf 1901 die Nadel 3408 mal und erreichte damit
die ersten sechs Nachkommastellen von ![]() , nämlich 3,1415929. R. Wolf (1850) erreichte in Zürich
mit 5000 Würfen den Wert 3,1596 (siehe Handbuch der Astronomie
S.127; Mitteilungen der Berner Naturf. Gesellschaft 1850; S.85 und 209;
zitiert nach Castellanos 1988, S.157f.), Smith (1855) mit 3204 Würfen
3,1553 und Fox (1894) mit 1120 Würfen für
, nämlich 3,1415929. R. Wolf (1850) erreichte in Zürich
mit 5000 Würfen den Wert 3,1596 (siehe Handbuch der Astronomie
S.127; Mitteilungen der Berner Naturf. Gesellschaft 1850; S.85 und 209;
zitiert nach Castellanos 1988, S.157f.), Smith (1855) mit 3204 Würfen
3,1553 und Fox (1894) mit 1120 Würfen für ![]() den Wert 3,1419. (vgl. Mäder 1989, S.54)
den Wert 3,1419. (vgl. Mäder 1989, S.54)
Ein Schüler von de Morgan soll bei 600 Versuchen den Wert 3,137
für ![]() erhalten haben.
erhalten haben.
Man kann ![]() aber nicht nur "erstechen",
sondern auch "erschießen". Das folgende Verfahren beschrieb
A. K. DEWDNEY 1988 (S.56ff.)
aber nicht nur "erstechen",
sondern auch "erschießen". Das folgende Verfahren beschrieb
A. K. DEWDNEY 1988 (S.56ff.)
![]() wird approximiert, indem man einem
Quadrat einen Viertelkreis einschreibt und hernach mit Zufallspunkten "beschießt".
Das Verhältnis der Punkte, die innerhalb des Kreisbogens liegen, zur
Gesamtzahl der abgegebenen Schüsse nähert sich bei wachsender
Schußzahl dem Verhältnis der Flächeninhalte von Viertelkreis
und Quadrat. Folglich kann man sich
wird approximiert, indem man einem
Quadrat einen Viertelkreis einschreibt und hernach mit Zufallspunkten "beschießt".
Das Verhältnis der Punkte, die innerhalb des Kreisbogens liegen, zur
Gesamtzahl der abgegebenen Schüsse nähert sich bei wachsender
Schußzahl dem Verhältnis der Flächeninhalte von Viertelkreis
und Quadrat. Folglich kann man sich ![]() aus diesem Verhältnis berechnen.
aus diesem Verhältnis berechnen.
Am einfachsten ist es, dieses Verfahren am Computer mittels einer geeigneten Programmiersprache zu simulieren. Das nachfolgende Turbo-Pascal Programm ist ausführlich kommentiert, doch die Grundstruktur soll hier noch einmal skizziert werden:
Am Bildschirm wird ein Quadrat gezeichnet, dem ein Viertelkreisbogen eingeschrieben
wird. Nun "beschießt" man dieses Quadrat mit Zufallspunkten.
Dazu läßt man den Computer mit Hilfe eines Zufallszahlengenerators
Werte für die x-Koordinate und y-Koordinate des Punktes im Intervall
[0;1] finden. Anschließend wird der Punkt am Bildschirm eingezeichnet,
sodaß man die Verteilung selbst auf "Zufälligkeit"
überprüfen kann, und der Zähler schuesse erhöht.
(Selbstverständlich kann auch der Computer keine echten Zufallszahlen
finden. Vielmehr ermittelt er aus Datum, Uhrzeit und einem geeigneten Algorithmus
eine Pseudozufallszahl, deren Qualität aber durch die graphische Darstellung
überprüfbar wird. Sollten sich nämlich bestimmte Muster
am Bildschirm erkennen lassen, so liegt ein schlechter Zufallszahlengenerator
vor. In der aktuellen Turbo-Pascal Version 7.0 ist mir das aber nicht
aufgefallen.) Die Entfernung vom Mittelpunkt M läßt sich
nun mit Hilfe des pythagoreischen Lehrsatzes berechnen: ![]() . Da man als Radius 1 E angenommen hat, kann man sich das Wurzelziehen
ersparen, wodurch die Programmgeschwindigkeit optimiert wird. Ist d
nun kleiner als 1, so liegt der betreffende Punkt innerhalb des Viertelkreises
und der Zähler treffer wird erhöht. Alle zehn Schüsse
wird die neue Approximation für
. Da man als Radius 1 E angenommen hat, kann man sich das Wurzelziehen
ersparen, wodurch die Programmgeschwindigkeit optimiert wird. Ist d
nun kleiner als 1, so liegt der betreffende Punkt innerhalb des Viertelkreises
und der Zähler treffer wird erhöht. Alle zehn Schüsse
wird die neue Approximation für ![]() am Bildschirm ausgegeben. Das Programm schießt so lange, bis der
Benützer eine Taste drückt oder ein Überlauf des Schußzählers
droht.
am Bildschirm ausgegeben. Das Programm schießt so lange, bis der
Benützer eine Taste drückt oder ein Überlauf des Schußzählers
droht.
program PI_APPROXIMATION_NACH_DER_MONTE_CARLO_METHODE
uses crt, graph; {Textmodus- und Grafikbefehle einbinden
var
schuesse, treffer, mittex, mittey, anzeige :word
x, y:real; {Koordinaten des Schusses
ein:char; {Eingabepuffer
const
rad=100; {Radius des Viertelkreises angeben
function IntToStr(I:real;stellen, nachkomma:byte): String
{Umwandlung von Zahlen in strings. stellen gibt die Gesamtzahl der ausgegebenen Stellen, nachkomma die Zahl der
Nachkommastellen an
var S: string[11]
begin
Str(I:stellen:nachkomma, s)
IntToStr := S
end
procedure init; {Initialisierung des Grafikbildschirms und der Variablen
var karte, modus:integer
begin
detectgraph(karte, modus); {Grafikkarte identifizieren
initgraph(karte, modus, 'c:\tp\BGI'); {Grafikmodus initialisieren. Pfad zu den Treibern angeben!
setfillstyle(0, white); {Füllmodus Hintergrundfarbe setzen
mittex:=getmaxx div 2; {x-Koordinate der Bildschirmmitte
mittey:=getmaxy div 2; {y-Koordinate der Bildschirmmitte
end
procedure reset
begin
cleardevice
rectangle(mittex - rad - 1, mittey - rad - 1, mittex + rad + 1, mittey + rad + 1); {Quadrat, das ,beschossen" wird, zeichnen
arc(mittex - rad - 1, mittey + rad + 1, 0, 90, 2*rad + 2); {Viertelkreisbogen zeichnen
outtextxy(mittex - rad - 20, mittey + rad + 10, '(0|0)'); {Beschriftung
outtextxy(mittex + rad - 15, mittey + rad + 10, '(1|0)'); {der ,Zielscheibe"
outtextxy(mittex - rad - 20, mittey - rad - 15, '(0|1)'); {mit Koordinaten
outtextxy(mittex - 100, mittey + 140, 'Schüsse:')
outtextxy(mittex , mittey + 140, 'Treffer:')
outtextxy(mittex + 100, mittey + 140, 'Approximation für pi:')
outtextxy(mittex - 185, mittey - 160, 'pi-Approximation nach der Monte-Carlo-Methode')
outtextxy(mittex - 200, mittey + 180, 'Drücken Sie [pi] für Pause und Einzelschritt, ')
outtextxy(mittex - 104, mittey + 190, '[n] für Neustart und')
outtextxy(mittex - 104, mittey + 200, '[ESC], um zu beenden!')
randomize; {Zufallszahlengenerator initialisieren
ein:=chr(32)
anzeige:=10
schuesse:=0
treffer:=0; {Variable zurücksetzen
end
procedure schiessen
begin
x:=random; {x-Koordinate zufällig im Intervall [0;1] ermitteln
y:=random; {y-Koordinate zufällig im Intervall [0;1] ermitteln
putpixel(round(mittex - rad + x*2*rad), round(mittey + rad - y*2*rad), lightblue); {Punkt den Koordinaten entsprechend am
Bildschirm setzen
inc(schuesse); {Schußzähler erhöhen
if (x*x + y*y) < 1 then inc(treffer); {Innerhalb des Viertelkreises? Dann Zähler erhöhen
end
procedure approximieren; {Anzahl der Schüsse und die Approximation für pi ausgeben
begin
bar(mittex - 100, mittey + 140 + 10, mittex - 100 + 38, mittey + 140 + 16)
outtextxy(mittex - 100, mittey + 140 + 10, inttostr(schuesse, 5, 0))
bar(mittex , mittey + 140 + 10, mittex + 38, mittey + 140 + 16)
outtextxy(mittex , mittey + 140 + 10, inttostr(treffer, 5, 0))
bar(mittex + 100, mittey + 140 + 10, mittex + 100 + 65, mittey + 140 + 16)
outtextxy(mittex + 100, mittey + 140 + 10, inttostr(treffer/schuesse*4, 8, 6))
end
begin
init; {Initialisierung aufrufen
repeat
reset
repeat
schiessen; {Quadrat beschießen
if schuesse mod anzeige=0 then approximieren; {alle 10 Schüsse pi berechnen
if keypressed then ein:=readkey
if ein='pi' then begin
ein:=readkey
anzeige:=1
end else anzeige:=10
until (ein in ['n',chr(27)]) or (schuesse=65535);
{bei Tastendruck oder vor Überlauf abbrechen
until ein=chr(27)
closegraph; {In Textmodus zurückkehren
end.
Bei drei Programmdurchläufen zu je 10 000 Schüssen erhielt ich beispielsweise die Näherungen 3,146162 , 3,164279 und 3,169600.
Die große Anzahl an Dezimalstellen von ![]() , die man durch Verwendung von Computern berechnen kann, stellt eine "Spielwiese"
für Statistiker und der Zahlenmystik verfallene Mathematiker dar.
Zwei erstaunliche Entdeckungen sollen hier nur beispielhaft angeführt
werden.
, die man durch Verwendung von Computern berechnen kann, stellt eine "Spielwiese"
für Statistiker und der Zahlenmystik verfallene Mathematiker dar.
Zwei erstaunliche Entdeckungen sollen hier nur beispielhaft angeführt
werden.
T.E. Lobeck aus Minneapolis stieß auf das folgende magische Quadrat,
in dem die Zahlen von 1 bis 25 eingetragen sind. Sodann setzte er die entsprechende
Stellen von ![]() ein und bemerkte zu seiner
Überraschung, daß der Summe jeder Zeile die Summe einer Spalte
entspricht. (vgl. Castellanos 1988, S.81)
ein und bemerkte zu seiner
Überraschung, daß der Summe jeder Zeile die Summe einer Spalte
entspricht. (vgl. Castellanos 1988, S.81)
| 17 | 24 | 1 | 8 | 15 | 65 |
|---|---|---|---|---|---|
| 23 | 5 | 7 | 14 | 16 | 65 |
| 4 | 6 | 13 | 20 | 22 | 65 |
| 10 | 12 | 19 | 21 | 3 | 65 |
| 11 | 18 | 25 | 2 | 9 | 65 |
| 65 | 65 | 65 | 65 | 65 |
| 2 | 4 | 3 | 6 | 9 | 24 |
|---|---|---|---|---|---|
| 6 | 5 | 2 | 7 | 3 | 23 |
| 1 | 9 | 9 | 4 | 2 | 25 |
| 3 | 8 | 8 | 6 | 4 | 29 |
| 5 | 3 | 3 | 1 | 5 | 17 |
| 17 | 29 | 25 | 24 | 23 |
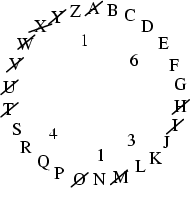
Martin GARDNER erwähnte in einem persönlichen
Gespräch mit Dario CASTELLANOS 1988 (S.81)
folgende Kuriosität, die James Davis entdeckte.
Wenn man alle Buchstaben des lateinischen Alphabets in einem Kreis aufschreibt
und jene, die eine vertikale Symmetrie besitzen, durchstreicht, so bleiben
Gruppen zu 3, 1, 4, 1, und 6 Buchstaben übrig. Dies sind aber gerade
die ersten fünf Ziffern des (gerundeten) Wertes von ![]() .
.
![]() ist, entsprechend dem Beweis von
Lindemann, eine transzendente Zahl. Das bedeutet, daß die Ziffernfolge
von
ist, entsprechend dem Beweis von
Lindemann, eine transzendente Zahl. Das bedeutet, daß die Ziffernfolge
von ![]() nicht periodisch ist und keinem
Gesetz gehorcht, sondern nur einer "Zufallsverteilung" folgt.
Daher müßte es irgendwo in diesem unendlichen Dezimalbruch einen
Abschnitt geben, der diesen Satz, dieses Kapitel und diese Fachbereichsarbeit
in codierter Form enthält. Dieser Gedanke läßt sich aber
auch für größere "Datenmengen", wie die Encyclopaedia
Britannica, fortspinnen und in letzter Konsequenz kann man das Paradoxon
und die Vermutung wagen, daß es in der Ziffernfolge von
nicht periodisch ist und keinem
Gesetz gehorcht, sondern nur einer "Zufallsverteilung" folgt.
Daher müßte es irgendwo in diesem unendlichen Dezimalbruch einen
Abschnitt geben, der diesen Satz, dieses Kapitel und diese Fachbereichsarbeit
in codierter Form enthält. Dieser Gedanke läßt sich aber
auch für größere "Datenmengen", wie die Encyclopaedia
Britannica, fortspinnen und in letzter Konsequenz kann man das Paradoxon
und die Vermutung wagen, daß es in der Ziffernfolge von ![]() Abschnitte für jedes Buch geben müßte, das jemals geschrieben
wurde, geschrieben wird oder in Zukunft geschrieben werden könnte!
(vgl. Gardner 1973, S.73f.)
Abschnitte für jedes Buch geben müßte, das jemals geschrieben
wurde, geschrieben wird oder in Zukunft geschrieben werden könnte!
(vgl. Gardner 1973, S.73f.)
Der Sinn der Berechnung extrem vieler Stellen von ![]() läßt sich mit zwei Sachverhalten erklären. Erstens bietet
die Untersuchung der Dezimalbruchentwicklung von
läßt sich mit zwei Sachverhalten erklären. Erstens bietet
die Untersuchung der Dezimalbruchentwicklung von ![]() die Möglichkeit, die "Zufälligkeit" der Verteilung
der zehn Ziffern in der Ziffernfolge von
die Möglichkeit, die "Zufälligkeit" der Verteilung
der zehn Ziffern in der Ziffernfolge von ![]() zu untersuchen. Außerdem bieten entsprechende Computerprogramme eine
sehr effiziente Methode, die Hardware der Computer zu testen, da schon
ein kleiner Rechenfehler große Folgen hat und viele falsche Stellen
erzeugt. (vgl. Peitgen 1992, S.181)
zu untersuchen. Außerdem bieten entsprechende Computerprogramme eine
sehr effiziente Methode, die Hardware der Computer zu testen, da schon
ein kleiner Rechenfehler große Folgen hat und viele falsche Stellen
erzeugt. (vgl. Peitgen 1992, S.181)
(Die Konvergenzgeschwindigkeit bedeutet hier die Anzahl der Glieder, die benötigt wird, um 3 Dezimalstellen von pi zu bestimmen. Es wurden auf Grund des hohen Programmieraufwandes aber nicht alle Algorithmen berücksichtigt.)
| Erfinder | Jahr | Term | Konvergenzgeschwindigkeit |
|---|---|---|---|
| Vieta | 1592 | 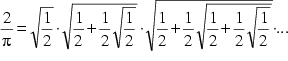 | 7 Glieder |
| Wallis | 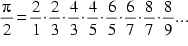 | 3857 Glieder | |
| Lord William Brouncker | 1630-1684 | 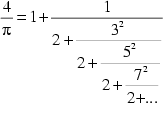 | |
| Newton | 1666 | 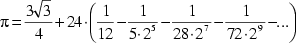 | |
| Gregory (1683-1675) und Leibniz | 1673 | 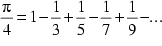 | 2455 Glieder |
| Gregory und Sharp | um 1700 | 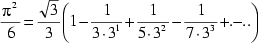 | |
| Euler | 18. Jhdt. | 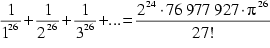 | |
| selbiger | 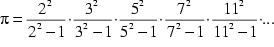 | ||
| selbiger | 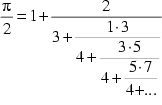 | ||
| selbiger(Euler1) | 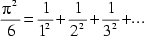 | 1612 Glieder | |
| selbiger(Euler2) | 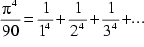 | 8 Glieder | |
| C. F. Gauß (1777-1855) | 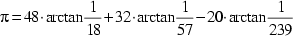 | ||
| Ramanujan (1887-1920) | 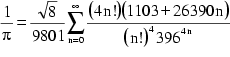 |
| Mathematiker | Jahr | berechnete Stellen | falsche Stellen |
|---|---|---|---|
| Vieta | 1580 | 10 Stellen | alle korrekt |
| van Roomen | um 1600 | 15 Stellen | |
| van Ceulen | um 1605 | 35 Stellen | |
| Abraham Sharp (1651-1742) | 1706 | 72 Stellen | |
| John Machin | 1707 | 100 Stellen | |
| Thomas de Lagny | 1719 | 127 Stellen | |
| Georg von Vega(1756-1802) | 1793 | 140 Stellen | ab der 137. Stelle |
| Thibaut | 1822 | 156 Stellen | |
| William Rutherford | 1841 | 208 Stellen | ab der 153. Stelle |
| Zacharias Dase | 1844 | 200 Stellen | |
| Thomas Clausen(1801-1885) | 1847 | 248 Stellen | |
| William Rutherford | 1853 | 440 Stellen | |
| Prof. Richter (Elbing) | 1855 | 500 Stellen | |
| William Shanks (GB) | 1874 | 707 Stellen | ab der 527. Stelle |
| D. F. Ferguson (GB) | 1946 | 730 Stellen | |
| John W. Wrench Jr. und Levi B. Smith | 1947 | 808 Stellen | |
| G. W. Reitwieser (USA) auf ENIAC | 1949 | 2 035 Stellen | |
| S. C. Nicholson und J. Jeenel auf NORC | 1954 | 3 089 Stellen | |
| Felton auf Pegasus | 1958 | 10 000 Stellen | |
| F. Genuis (Paris) auf IBM 704 | 1958 | 10 000 Stellen | |
| J. M. Gerard (London) auf IBM 7090 | 1961 | 20 000 Stellen | |
| Daniel Shanks und John W. Wrench Jr. auf IBM 7090 | 1961 | 100 265 Stellen | |
| Guilloud und Bouyer auf CDC 7600 | 1973 | 1 000 000 Stellen | |
| Yoshiaki Tamura und Yasuma Kanada (Japan) auf HITAC M-280H | 1983 | 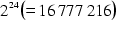 Stellen Stellen | |
| Gosper auf Symbolics | 1985 | 17 000 000 Stellen | |
| D. H. Bailey auf Cray-2 | 1986 | 29 360 000 Stellen | |
| Kanada auf SX 2 | 1987 | 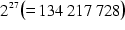 Stellen Stellen | |
| Kanada | 1988 | 201 326 000 Stellen | |
| Kanada auf HITAC S-820/80 | 1989 | 1 073 740 000 Stellen |
Die Form des Kreises beschäftigt die Menschen seit Jahrtausenden,
denn spätestens seit der Erfindung des Rades , die sich die Eigenschaft,
daß dessen Umfang endlich aber unbegrenzt ist, zunutze macht, haben
Mathematiker immer wieder versucht, den Umfang oder auch den Flächeninhalt
von Kreisen exakt zu bestimmen. Die Geschichte der Approximationen der
Zahl ![]() ist deshalb auch ursächlich
mit den Versuchen, den Kreis zu "quadrieren", verbunden. Dieses
Problem gehörte mit zu den drei berühmten der Antike: "Würfelverdopplung",
"Winkeldreiteilung" und "Quadratur des Kreises".
ist deshalb auch ursächlich
mit den Versuchen, den Kreis zu "quadrieren", verbunden. Dieses
Problem gehörte mit zu den drei berühmten der Antike: "Würfelverdopplung",
"Winkeldreiteilung" und "Quadratur des Kreises".
Diese Fachbereichsarbeit soll nun einen Überblick über die
Versuche verschiedenster Kulturen, ![]() zu berechnen, bieten, wobei an Hand ausgewählter Beispiele besonders
effektive oder bemerkenswerte Methoden gezeigt werden. Dabei lassen sich
die Weiterentwicklung in der Rechentechnik und die Verfeinerung der Methoden
von den Hochkulturen in Ägypten und Babylonien über das antike
Griechenland, Mittelalter und Neuzeit bis ins Computerzeitalter heute beobachten.
Darum dient ein einfaches Turbo-Pascal-Programm der Simulation einer Monte-Carlo-Methode
zur Bestimmung von
zu berechnen, bieten, wobei an Hand ausgewählter Beispiele besonders
effektive oder bemerkenswerte Methoden gezeigt werden. Dabei lassen sich
die Weiterentwicklung in der Rechentechnik und die Verfeinerung der Methoden
von den Hochkulturen in Ägypten und Babylonien über das antike
Griechenland, Mittelalter und Neuzeit bis ins Computerzeitalter heute beobachten.
Darum dient ein einfaches Turbo-Pascal-Programm der Simulation einer Monte-Carlo-Methode
zur Bestimmung von ![]() .
.
Weiters wird die immer exaktere Bestimmung des Werts von ![]() aufgezeigt, was schließlich zur Frage nach deren Sinnhaftigkeit führt.
Eine tabellarische Aufzählung einiger Reihen, Produkte und Reihenbruchentwicklungen
bietet einen Überblick über die zur Approximation von
aufgezeigt, was schließlich zur Frage nach deren Sinnhaftigkeit führt.
Eine tabellarische Aufzählung einiger Reihen, Produkte und Reihenbruchentwicklungen
bietet einen Überblick über die zur Approximation von ![]() geeigneten Terme und eine Tabelle mit den zur jeweiligen Zeit bekannten
Dezimalstellen von
geeigneten Terme und eine Tabelle mit den zur jeweiligen Zeit bekannten
Dezimalstellen von ![]() faßt die Geschichte
der Approximationen noch einmal zusammen. Das im Anhang beigefügte
zweite Turbo-Pascal-Programm hat die Aufgabe, die Konvergenzgeschwindigkeit
der aufgelisteten Terme zu bestimmen, so weit dies auf Grund der internen
Rechengenauigkeit möglich ist.
faßt die Geschichte
der Approximationen noch einmal zusammen. Das im Anhang beigefügte
zweite Turbo-Pascal-Programm hat die Aufgabe, die Konvergenzgeschwindigkeit
der aufgelisteten Terme zu bestimmen, so weit dies auf Grund der internen
Rechengenauigkeit möglich ist.
Das folgende Turbo-Pascal 7.0 Programm diente mir dazu die Konvergenzgeschwindigkeit der in obiger Tabelle angegebenen unendlichen Reihen und Produkte zu bestimmen.
program Piapproximationen
uses crt
procedure init
begin
textattr:=$0f;clrscr
writeln(' Approximationen von pi')
window(1,2,80,50);textattr:=$49;clrscr
window(2,3,79,39);textattr:=$07;clrscr;window(2,41,79,49);textattr:=$1f;clrscr
textattr:=$17;writeln
write(' Gliederzahl Näherung für pi Differenz')
writeln;writeln;writeln;writeln;textattr:=$4f
write(' "Genauer" Wert für pi: ',pi:19:17);clreol
end
function eingabe(text:string;x,y:byte):char
var taste:char
begin
gotoxy(x,y)
textattr:=$07
write(text,' ');write(chr(8))
textattr:=$0f
if keypressed then taste:=readkey
taste:=readkey
eingabe:=taste
write(taste)
if keypressed then taste:=readkey
end
procedure auswahl(var approx,stellen:byte)
var ein:char
begin
window(2,3,79,39);textattr:=$07
writeln
writeln(' Mit welchem Algorithmus wollen Sie die Berechnung durchführen?')
writeln
writeln(' A. Vieta')
writeln(' B. Wallis')
writeln(' C. Leibniz')
writeln(' D. Sharp')
writeln(' E. Euler 1')
writeln(' F. Euler 2')
writeln
repeat ein:=eingabe('Ihre Wahl:',22,13) until ein in ['a'..'f','A'..'F']
if ein in ['a'..'f'] then approx:=ord(ein)-96 else approx:=ord(ein)-64
writeln;writeln;writeln;textattr:=$07
writeln(' Wieviele Stellen (1-8) möchten Sie berechnen?')
repeat ein:=eingabe('Ihre Wahl:',22,18) until ein in ['1'..'8']
stellen:=ord(ein)-48
end
function beenden:boolean
var ein:char
begin
window(2,30,79,39);textattr:=$07
writeln(' Wollen Sie noch eine Berechnung durchführen [R] oder beenden [E]?')
writeln
repeat ein:=eingabe('Ihre Wahl:',22,3) until ein in ['r','R','e','E']
if ein in ['e','E'] then beenden:=true else beenden:=false
clrscr
end
procedure ausgabe(n:longint;wert:real)
begin
window(2,41,79,49)
textattr:=$1f
gotoxy(4,5)
write(n:8,' ',wert:19:17,' ',wert-pi:20:17)
end
procedure berechnung(term,stellen:byte)
var t_1,e:real
n:longint
ein:char
vorherok:boolean
function potenz (Basis: integer; expon: integer):real
var i:integer
pot:real
begin
if expon = 0 then potenz := 1
else begin
pot:=1
for i:=1 to expon do begin
pot:=pot*basis
end
potenz:=pot
end
end
function FAKUL(x:integer):real
begin
if x<=1 then fakul:=x
else fakul:=x*fakul(x-1)
end
function stellenok:boolean
begin
if trunc(e*potenz(10,stellen))=trunc(pi*potenz(10,stellen))
then stellenok:=true
else stellenok:=false
end
function vieta(glied:longint):real
begin
if glied=1 then vieta:=sqrt(0.5)
else vieta:=sqrt(0.5+0.5*vieta(glied-1)); {rekursive Programmierung!
end
function wallis(glied:longint):real
begin
wallis:=(glied+glied mod 2)/(glied+(glied+1) mod 2)
end
function leibniz(glied:longint):real
begin
leibniz:=potenz(-1,(glied+1) mod 2)/(2*glied-1)
end
function sharp(glied:longint):real
begin
sharp:=potenz(-1,(glied+1) mod 2)/((2*n-1)*potenz(3,n-1))
end
function euler1(glied:longint):real
begin
euler1:=1/sqr(glied)
end
function euler2(glied:longint):real
begin
euler2:=1/glied/glied/glied/glied
end
begin
ein:=readkey
e:=1
n:=1
case term of
1:t_1:=vieta(1)
2:t_1:=wallis(1)
3:t_1:=leibniz(1)
4:t_1:=sharp(1)
5:t_1:=euler1(1)
6:t_1:=euler2(1)
end
repeat
vorherok:=stellenok
inc(n)
case term of
1:begin
t_1:=t_1*vieta(n)
e:=2/t_1
end
2:begin
t_1:=t_1*wallis(n)
e:=t_1*2
end
3:begin
t_1:=t_1+leibniz(n)
e:=t_1*4
end
4:begin
t_1:=t_1+sharp(n)
e:=2*sqrt(3)*t_1
end
5:begin
t_1:=t_1+euler1(n)
e:=sqrt(t_1*6)
end
6:begin
t_1:=t_1+euler2(n)
e:=sqrt(sqrt(t_1*90))
end
end
ausgabe(n,e)
until stellenok and vorherok
end
procedure menue
var term,stellen:byte
begin
repeat
auswahl(term,stellen)
berechnung(term,stellen)
until beenden
end
BEGIN
init
menue
END.
Ich erkläre, daß ich diese Fachbereichsarbeit selbst verfaßt habe und daß außer der angegebenen Literatur keine weitere verwendet wurde.
 | |
| |