 |
(6.9) |
Let us assume a one dimensional stochastic differential equation with multiplicative noise [41]
The increment 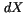 during a short time interval
during a short time interval 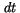 is given by
is given by
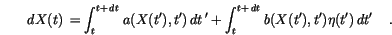
![$[t,t+\,d{t}\,]$](img241.gif) , multiply it by the length of the interval and use the result as the increment for small
, multiply it by the length of the interval and use the result as the increment for small 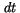 . Thus, we obtain
. Thus, we obtain
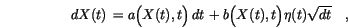
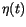 is a standard Gaussian random variable at each discrete time step with
is a standard Gaussian random variable at each discrete time step with
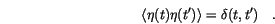
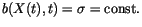 , that is the case for additive noise, it is equivalent to equation (
, that is the case for additive noise, it is equivalent to equation (
However, we could also evaluate the integrand 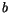 at any other time
at any other time  in the interval
in the interval
![$[t,t+\,d{t}\,]$](img241.gif) and at
and at
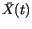 |
 |
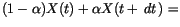 |
|
 |
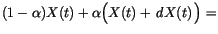 |
||
 |
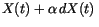 |
(6.10) |
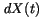 an implicit expression
an implicit expression
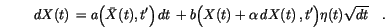
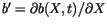 we get
we get
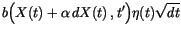 |
 |
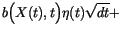 |
|
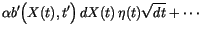 |
|||
 |
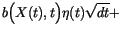 |
||
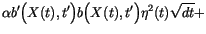 |
|||
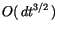 |
(6.11) |
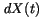
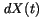 |
 |
![$\displaystyle \left[
a\Bigl(X(t),t\Bigr) +
\alpha b'\Bigl(X(t),t\Bigr)b\Bigl(X(t),t\Bigr) \eta^2(t)
\right] \,d{t}\, +$](img267.gif) |
|
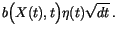 |
(6.12) |
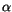 and
and 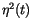 . The latter can be replaced by 1 for terms up to the order of
. The latter can be replaced by 1 for terms up to the order of 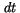 . Depending on the choice of
. Depending on the choice of 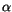 and the interpretation of the integral, we get different drift terms.
and the interpretation of the integral, we get different drift terms.
If we set 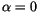 , we get
, we get
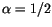 , we get
, we get
Thus, we have to distinguish between the interpretation of a stochastic differential equation and the version, in which it is written.
The stochastic differential equation (![]() ) can be written in an Itô version using (
) can be written in an Itô version using (![]() ) as
) as
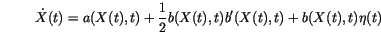 |
(6.17) |
Reversely, (![]() ) can be written in a Stratonovich version as
) can be written in a Stratonovich version as
Due to the different drift terms, the two interpretations yield different dynamical properties [41]. Itô calculus is commonly chosen on certain mathematical grounds, since rather general results of probability theory can then be employed. On the other hand, white noise is usually an idealization of physical (coloured) noise with short autocorrelation time, in which case the two time covariance function is given by
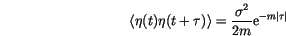
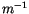 .
.
The Wong-Zakai-Theorem [42] then says, that in the formal zero-correlation-time limit