8.1.1
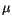 mag standard problem #3
mag standard problem #3
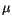 mag standard problem #3
mag standard problem #3
This problem has been chosen to verify the equilibrium states obtained by the finite difference program. A lattice of
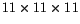 magnetic moments and the fixpoint iteration method (section
magnetic moments and the fixpoint iteration method (section ![]() ) have been used to calculate the equilibrium states.
) have been used to calculate the equilibrium states.
The http://www.ctcms.nist.gov/ rdm/mumag.html mag standard problem #3 [48] consists in calculating the single domain limit of a cubic magnetic particle. This is the size of equal energy for the so-called flower state (fig.
mag standard problem #3 [48] consists in calculating the single domain limit of a cubic magnetic particle. This is the size of equal energy for the so-called flower state (fig. ![]() ) on the one hand, and the vortex or curling state (fig.
) on the one hand, and the vortex or curling state (fig. ![]() ) on the other hand. The easy axis of magnetocrystalline anisotropy is parallel to a principal axis of the cube. The uniaxial anisotropy constant is given by
) on the other hand. The easy axis of magnetocrystalline anisotropy is parallel to a principal axis of the cube. The uniaxial anisotropy constant is given by
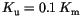 , where
, where
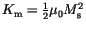 is a magnetostatic energy density.
is a magnetostatic energy density.
The results are given in the column marked ``FD'' in tables ![]() ,
, ![]() , and
, and ![]() and compared with those published by Rave et al. [49], Ribeiro et al. and Hertel et al. on the web page of NIST [48]. The partial energies are given in units of
and compared with those published by Rave et al. [49], Ribeiro et al. and Hertel et al. on the web page of NIST [48]. The partial energies are given in units of 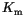 , the magnetization in units of
, the magnetization in units of 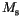 , and the single domain limit
, and the single domain limit 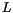 in units of
in units of
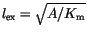 , where
, where 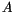 is the exchange constant.
is the exchange constant.