A rigid magnetic moment is an approximation for a very small magnetic particle with strong exchange interaction. If it is small enough, the exchange interaction will keep the magnetization uniform which leads to coherent rotation. In this reversal mode the constituent spins rotate in unison. The exchange interaction gives a constant contribution to the Landau free energy in this approximation and therefore does not influence the motion of the magnetization vector. These are the common assumptions in the Stoner-Wohlfarth model.
The undamped equation of motion (![]() ) describes the continuous precession of the magnetization vector around the direction of the effective magnetic field. However, changes of the magnetization are known from experiment to decay in finite time. Thus, damping is introduced by a phenomenological term. The commonly used Landau-Lifshitz equation of motion (
) describes the continuous precession of the magnetization vector around the direction of the effective magnetic field. However, changes of the magnetization are known from experiment to decay in finite time. Thus, damping is introduced by a phenomenological term. The commonly used Landau-Lifshitz equation of motion (![]() ) results in a spiraling movement of the magnetization vector towards its equilibrium direction. The analytical solution [50]
) results in a spiraling movement of the magnetization vector towards its equilibrium direction. The analytical solution [50]
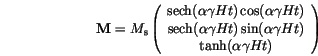
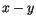 plane in figure
plane in figure 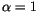 the precession is critically damped, and the magnetization turns ``directly'' into the direction of the effective field.
the precession is critically damped, and the magnetization turns ``directly'' into the direction of the effective field.
Figure ![]() shows, how the switching time depends on the value of the damping parameter. Initially, the magnetization vector points in a direction opposite to the effective field. A small deflection starts the reversal process. We can measure the switching time, which is the time, until the component of the magnetization parallel to the effective field has reached a certain value (e.g.
shows, how the switching time depends on the value of the damping parameter. Initially, the magnetization vector points in a direction opposite to the effective field. A small deflection starts the reversal process. We can measure the switching time, which is the time, until the component of the magnetization parallel to the effective field has reached a certain value (e.g. 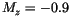 ). For
). For 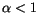 the motion of the magnetization vector is undercritically damped. It makes many precessions around the direction of the effective field. On the contrary, for
the motion of the magnetization vector is undercritically damped. It makes many precessions around the direction of the effective field. On the contrary, for 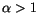 the motion is overcritically damped. The minimum of the switching time is found for
the motion is overcritically damped. The minimum of the switching time is found for 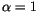 , which is the case of critical damping [51]. Table
, which is the case of critical damping [51]. Table ![]() shows the damping parameters for magnetic materials [50,52], which are commonly used in magnetic recording tapes. These values are obtained by ferromagnetic resonance experiments: A very strong external DC field keeps the magnetization of the sample homogeneous and parallel to its direction. A small AC field perpendicular to the DC field excites a periodic motion of the magnetization with a small amplitude. As the frequency of the AC field is varied, the absorbed energy varies and at the resonance frequency it reaches a maximum. From the width of the absorption spectrum, the damping constant can be derived.
shows the damping parameters for magnetic materials [50,52], which are commonly used in magnetic recording tapes. These values are obtained by ferromagnetic resonance experiments: A very strong external DC field keeps the magnetization of the sample homogeneous and parallel to its direction. A small AC field perpendicular to the DC field excites a periodic motion of the magnetization with a small amplitude. As the frequency of the AC field is varied, the absorbed energy varies and at the resonance frequency it reaches a maximum. From the width of the absorption spectrum, the damping constant can be derived.
The equilibrium direction of the magnetic moment is determined by the magnetocrystalline anisotropy axis and the direction of the external field. It can be readily obtained by considering the Landau free energy 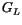 of the magnetic moment, which is in the case of uniaxial anisotropy given by
of the magnetic moment, which is in the case of uniaxial anisotropy given by
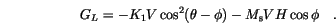
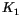 is the first magnetocrystalline anisotropy constant,
is the first magnetocrystalline anisotropy constant, 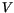 the volume of the magnetic particle,
the volume of the magnetic particle, 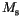 its saturation magnetization, and
its saturation magnetization, and 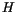 the external field. If an external field is applied at an angle
the external field. If an external field is applied at an angle 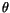 to the easy axis of the uniaxial anisotropy of the particle, the magnetization vector will reach its equilibrium position at an angle
to the easy axis of the uniaxial anisotropy of the particle, the magnetization vector will reach its equilibrium position at an angle 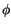 from the field direction, where the Landau free energy has a local minimum. Since there is not only one minimum the equilibrium direction is also influenced by the history of the magnetization vector. This effect is called hysteresis.
from the field direction, where the Landau free energy has a local minimum. Since there is not only one minimum the equilibrium direction is also influenced by the history of the magnetization vector. This effect is called hysteresis.
![\includegraphics[scale=0.6]{fig/sw_hyst.eps}](img514.gif)
|
Another important aspect can be explained using this simple model: The difference between reversible and irreversible magnetization processes. Reversible processes are those, in which the magnetization returns to its initial position after the perturbation has been removed again. For example, when a weak external bias field is applied, the magnetization will change slightly, but upon removal of the bias field, it returns to its initial position. However, if the bias field is strong enough, the magnetization can switch irreversibly and remain in a different energy minimum after the bias field has been switched off. Of course, this effect is used to switch the magnetization between different directions and store information thereby.
The ``energy landscape'' for a cobalt sphere with
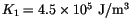 ,
,
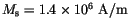 and a volume of
and a volume of
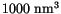 is given in figure
is given in figure ![]() . An external field of
. An external field of
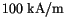 is applied at an angle of
is applied at an angle of 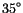 to the easy axis. One energy minimum is found for
to the easy axis. One energy minimum is found for
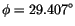 and a second for
and a second for
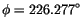 .
.