The interaction between the electron's magnetic moment and the crystal lattice has already been considered, when we introduced the damping term in the Landau-Lifshitz equation (section ![]() ). But this is not a one-way interaction, which transfers energy only from the spins to the lattice and causes the relaxation of the magnetization towards its equilibrium position. Energy can also be transferred from the lattice to the electrons. Thermal energy causes perturbations of the crystal lattice, which induces fluctuations of the magnetization distribution. We incorporate this thermal activation by a stochastic field, as described in section
). But this is not a one-way interaction, which transfers energy only from the spins to the lattice and causes the relaxation of the magnetization towards its equilibrium position. Energy can also be transferred from the lattice to the electrons. Thermal energy causes perturbations of the crystal lattice, which induces fluctuations of the magnetization distribution. We incorporate this thermal activation by a stochastic field, as described in section ![]() .
.
Thus, the magnetization wil not remain in its equilibrium direction but precess in a random walk around it (figure ![]() ). The mean distance from the equilibrium direction is determined by the temperature and the height of the potential barrier surrounding the energy minimum.
). The mean distance from the equilibrium direction is determined by the temperature and the height of the potential barrier surrounding the energy minimum.
If we consider a Stoner-Wohlfarth particle without an external field, its energy is given by
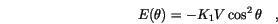
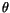 denotes the angle between the magnetization vector and the easy axis. In thermal equilibrium we expect the probability density for the angle
denotes the angle between the magnetization vector and the easy axis. In thermal equilibrium we expect the probability density for the angle 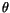 to give a Boltzmann distribution (
to give a Boltzmann distribution (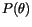 |
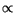 |
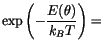 |
|
 |
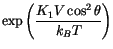 |
(9.1) |
![$[\theta, \theta+ \,d{\theta}\,]$](img529.gif) to the easy axis is given by
to the easy axis is given by
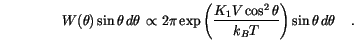
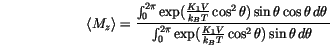

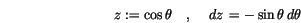
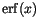 denotes the error function
denotes the error function
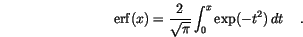
The distributions obtained by computer experiments are shown in figure ![]() . The experimentally obtained distribution of
. The experimentally obtained distribution of 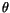 (the histogram bars in figure
(the histogram bars in figure ![]() ) is in excellent agreement with the analytically expected distribution. The time average for
) is in excellent agreement with the analytically expected distribution. The time average for 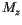 (fig.
(fig. ![]() ) is also in good agreement with the analytically expected values, which is obtained from (
) is also in good agreement with the analytically expected values, which is obtained from (![]() ). The time step size is 1/30th and 1/100th of the typical precession time of the magnetization vector in the effective field (cf. section
). The time step size is 1/30th and 1/100th of the typical precession time of the magnetization vector in the effective field (cf. section ![]() ).
).
However, as 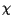 increases (temperature increases or the particle size or the anisotropy are decreased) the magnetization vector does not stay in its energy minimum. The thermal perturbation can be become strong enough to make it cross the energy barrier and jump into another energy minimum. In this case a magnetization reversal or switching event occurs. Figure
increases (temperature increases or the particle size or the anisotropy are decreased) the magnetization vector does not stay in its energy minimum. The thermal perturbation can be become strong enough to make it cross the energy barrier and jump into another energy minimum. In this case a magnetization reversal or switching event occurs. Figure ![]() shows, how the number of switching events depends on
shows, how the number of switching events depends on 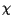 . The probability for the magnetization vector to surmount the energy barrier and escape into the other energy minimum is given by the classical Arrhenius formula of chemical reaction theory, which states, that it is proportional to
. The probability for the magnetization vector to surmount the energy barrier and escape into the other energy minimum is given by the classical Arrhenius formula of chemical reaction theory, which states, that it is proportional to

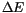 denotes the energy barrier, which is in our case given by the magnetocrystalline anisotropy energy. The fit of this law (since we do not know the prefactor) to the data is also given in figure
denotes the energy barrier, which is in our case given by the magnetocrystalline anisotropy energy. The fit of this law (since we do not know the prefactor) to the data is also given in figure
![\includegraphics[scale=0.6]{fig/sim090903_nswchi.eps}](img548.gif)
|
Of course, it depends on the measurement time, how many switching events are detected. No matter how small the temperature is (in a realistic model it will always be finite), a switching event can always occur. At lower temperatures or for larger particles it is just less likely, than for higher temperatures and smaller particles. If we wait for more than
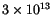 s (
s (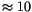 million years), we can measure the decay of magnetization in magnetic stone. The typical relaxation time is proportional to
million years), we can measure the decay of magnetization in magnetic stone. The typical relaxation time is proportional to 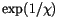 (cf. section
(cf. section ![]() ). Researchers in the field of rock magnetism study such phenomena, because the initial susceptibility is frequently used as a palaeoclimatic indicator in sediments [54,55]. If we want to store information on magnetic tape, the particles should be large enough and their anisotropy strong enough to have a relaxation time larger than
). Researchers in the field of rock magnetism study such phenomena, because the initial susceptibility is frequently used as a palaeoclimatic indicator in sediments [54,55]. If we want to store information on magnetic tape, the particles should be large enough and their anisotropy strong enough to have a relaxation time larger than 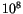 s (
s (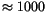 years). If the particles are still smaller, they might be suitable for the measurement of switching dynamics (cf. section
years). If the particles are still smaller, they might be suitable for the measurement of switching dynamics (cf. section ![]() ). Finally, if the relaxation time reaches the order of the Larmor precession period, the magnetization flips back and forth many times during the measurement time of experiments. Therefore in zero applied field, the measured average value of the magnetization will be zero. In figure
). Finally, if the relaxation time reaches the order of the Larmor precession period, the magnetization flips back and forth many times during the measurement time of experiments. Therefore in zero applied field, the measured average value of the magnetization will be zero. In figure ![]()
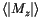 , the average of the absolute value of
, the average of the absolute value of 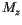 , has been plotted, because the average magnetization
, has been plotted, because the average magnetization
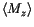 would vanish, as soon as switching events occur.
would vanish, as soon as switching events occur.
For very small relaxation times, an ensemble of magnetic particles behaves essentially like paramagnetic atoms. Thus, the magnetization can be described by a Langevin function and there is no hysteresis. But we find a very high saturation magnetization, because each particle behaves like a huge atom with 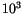 or even
or even 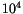 spins. A conventional paramagnet requires very high fields to reach saturation, because each atom carries only one spin. Since our magnetic particles carry a very large magnetic moment, the magnetic fields necessary to saturate the ensemble are easy to obtain. Hence, this phenomenon of the loss of ferromagnetism in small particles is known as superparamagnetism.
spins. A conventional paramagnet requires very high fields to reach saturation, because each atom carries only one spin. Since our magnetic particles carry a very large magnetic moment, the magnetic fields necessary to saturate the ensemble are easy to obtain. Hence, this phenomenon of the loss of ferromagnetism in small particles is known as superparamagnetism.