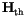 , which is added to the effective field (
, which is added to the effective field (
Thermal activation is introduced in the Landau-Lifshitz equation (![]() ) by a stochastic thermal field
) by a stochastic thermal field
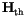 , which is added to the effective field (
, which is added to the effective field (![]() ). It accounts for the effects of the interaction of the magnetization with the microscopic degrees of freedom (eg. phonons, conducting electrons, nuclear spins, etc.), which cause fluctuations of the magnetization distribution. This interaction is also responsible for the damping, since fluctuations and dissipation are related manifestations of one and the same interaction of the magnetization with its environment.
). It accounts for the effects of the interaction of the magnetization with the microscopic degrees of freedom (eg. phonons, conducting electrons, nuclear spins, etc.), which cause fluctuations of the magnetization distribution. This interaction is also responsible for the damping, since fluctuations and dissipation are related manifestations of one and the same interaction of the magnetization with its environment.
Since a large number of microscopic degrees of freedom contribute to this mechanism, the thermal field is assumed to be a Gaussian random process with the following statistical properties:
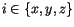 of space.
The second moment, or variance, is given by
of space.
The second moment, or variance, is given by
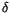 expresses the assumption, that the different components of the thermal field are uncorrelated, whereas the Dirac
expresses the assumption, that the different components of the thermal field are uncorrelated, whereas the Dirac 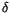 expresses, that the autocorrelation time of the thermal field is much shorter than the response time of the system (``white noise'', cf. section
expresses, that the autocorrelation time of the thermal field is much shorter than the response time of the system (``white noise'', cf. section
After adding the thermal field we get the stochastic Landau-Lifshitz equation
To keep the notation simple, we rewrite (![]() ) by substituting
) by substituting
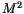 for
for
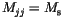 . We have used the Einstein summation convention and we will do so in the following. The outer products have been rewritten with the totally antisymmetric unit tensor
. We have used the Einstein summation convention and we will do so in the following. The outer products have been rewritten with the totally antisymmetric unit tensor 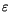 (Levi-Civita symbol).
(Levi-Civita symbol).
Hence, we can simplify the stochastic Landau-Lifshitz equation (![]() ) and get
) and get
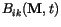 for the stochastic process
for the stochastic process
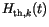 is a function of
is a function of 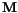 .
.