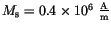 and
and
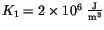 ,
,
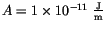 . In all simulations the number of switching events was counted for at least 100 ns up to 1
. In all simulations the number of switching events was counted for at least 100 ns up to 1  s and the results extrapolated to 1
s and the results extrapolated to 1 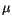 s.
s.
Cubes are easy to handle with finite difference packages, because they have no curved boundaries. Thus, cubic particles are good candidates to compare the results of the finite difference program with those of the finite element package. In addition the results are compared with those of Nakatani et al. [56], whose material parameters have been used. They are chosen as
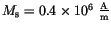 and
and
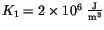 ,
,
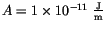 . In all simulations the number of switching events was counted for at least 100 ns up to 1
. In all simulations the number of switching events was counted for at least 100 ns up to 1 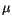 s and the results extrapolated to 1
s and the results extrapolated to 1 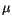 s.
s.
Figure ![]() shows the time dependence of the magnetization for a cubic particle of 32 nm edge length at 300 K. The magnetization fluctuates in the energy minimum around
shows the time dependence of the magnetization for a cubic particle of 32 nm edge length at 300 K. The magnetization fluctuates in the energy minimum around 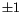 . From time to time reversal processes occur when the magnetization crosses the energy barrier and switches to the other energy minimum. The probability per unit time, that
. From time to time reversal processes occur when the magnetization crosses the energy barrier and switches to the other energy minimum. The probability per unit time, that 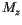 jumps over the energy barrier
jumps over the energy barrier 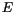 in thermal equilibrium, is proportional to
in thermal equilibrium, is proportional to

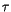 which can thus be written in the form of the Arrhenius-Néel law [57]
which can thus be written in the form of the Arrhenius-Néel law [57]
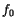 is the characteristic dynamic frequency. The original estimation of Néel was
is the characteristic dynamic frequency. The original estimation of Néel was
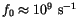 , but recently it has become more customary to take
, but recently it has become more customary to take
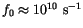 up to
up to
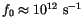 .
As we will see, the characteristic dynamic frequency depends on the damping constant, which is a material parameter.
.
As we will see, the characteristic dynamic frequency depends on the damping constant, which is a material parameter.
The number of reversal processes should, of course, be independent of the time discretization. This has been verified and the results are shown in figure ![]() for a
for a
 discretization. As the time step is decreased from
discretization. As the time step is decreased from 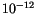 s to
s to
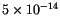 s, the number of switching events increases and converges. Then, the space discretization dependence is investigated (fig.
s, the number of switching events increases and converges. Then, the space discretization dependence is investigated (fig. ![]() ) and we find for three different space discretizations (
) and we find for three different space discretizations (
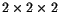 ,
,
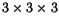 ,
,
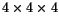 ) consistent results (within fluctuations due to the stochastic nature of the underlying processes).
) consistent results (within fluctuations due to the stochastic nature of the underlying processes).
In addition, the results for a finite element model are plotted in figure ![]() . The cube has been discretized into 64 nodes and 135 tetrahedral elements and the results are in excellent agreement with those of the finite difference model.
. The cube has been discretized into 64 nodes and 135 tetrahedral elements and the results are in excellent agreement with those of the finite difference model.
If we fit the data of the smallest time step in the linear region in figure ![]() with the Arrhenius-Néel law, we find a characteristic dynamic frequency of
with the Arrhenius-Néel law, we find a characteristic dynamic frequency of
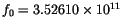 . The exponent is
. The exponent is
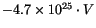 and it is in good agreement with the value
and it is in good agreement with the value
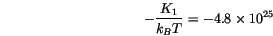
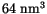 particle and we see, that the particle switches coherently.
particle and we see, that the particle switches coherently.
|
[Initial magnetization ( 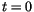 ps)] ps)]
![\includegraphics[scale=0.25]{fig/m000.eps}](img598.gif) [Thermally perturbed magnetization distribution (
[Thermally perturbed magnetization distribution (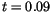 ps)] ps)]
![\includegraphics[scale=0.25]{fig/m048.eps}](img600.gif) [Switching starts (
[Switching starts (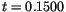 ps)] ps)]
![\includegraphics[scale=0.25]{fig/m080.eps}](img602.gif) [The reversal process progresses (
[The reversal process progresses (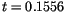 ps)] ps)]
![\includegraphics[scale=0.25]{fig/m083.eps}](img604.gif) [Crossing the energy barrier (
[Crossing the energy barrier (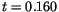 ps)] ps)]
![\includegraphics[scale=0.25]{fig/m085.eps}](img606.gif) [Reversal process completed (
[Reversal process completed (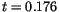 ps)] ps)]
![\includegraphics[scale=0.25]{fig/m094.eps}](img608.gif)
|
The characteristic dynamic frequency obtained above is quite high compared to the estimate of Néel. However, it is a question of the definition of a switching event. This fact is illustrated in figure ![]() . If the magnetization changes its sign and its absolute value exceeds
. If the magnetization changes its sign and its absolute value exceeds
 , then a switching event is counted. For
, then a switching event is counted. For
 we get a number of switching events which is one order of magnitude larger than that for
we get a number of switching events which is one order of magnitude larger than that for
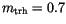 . This is due to the fact, that there are many switching events, in which the magnetization does not complete a full reversal, but it already switches back at an earlier stage. Such events can also be identified in figure
. This is due to the fact, that there are many switching events, in which the magnetization does not complete a full reversal, but it already switches back at an earlier stage. Such events can also be identified in figure ![]() , where we find ``spikes'' of incomplete switching events. Thus, the characteristic dynamic frequency depends on the definition of a switching event. The exponent of the Arrhenius-Néel law is not influenced, since the slope of the graphs in figure
, where we find ``spikes'' of incomplete switching events. Thus, the characteristic dynamic frequency depends on the definition of a switching event. The exponent of the Arrhenius-Néel law is not influenced, since the slope of the graphs in figure ![]() remains the same.
remains the same.
Physically interesting is the dependence on the damping constant, because this is a material parameter, which can be obtained from ferromagnetic resonance experiments (cf. section ![]() ). As the damping constant is increased from
). As the damping constant is increased from 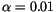 , the number of switching events increases, too. At a temperature of 0 K the reversal time of a fine particle is proportional to
, the number of switching events increases, too. At a temperature of 0 K the reversal time of a fine particle is proportional to
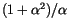 [51]. Therefore, it is reasonable, that the characteristic dynamic frequency is proportional to
[51]. Therefore, it is reasonable, that the characteristic dynamic frequency is proportional to
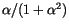 . The solid line in figure
. The solid line in figure ![]() is a fit of the
is a fit of the
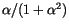 law to the data obtained by computer simulations (circles).
law to the data obtained by computer simulations (circles).
|
[Time step dependence]
![\includegraphics[scale=0.45]{fig/nakatstep.eps}](img615.gif) [Discretization dependence]
[Discretization dependence]
![\includegraphics[scale=0.45]{fig/nakatdiscret.eps}](img616.gif) [Dependence on definition of switching]
[Dependence on definition of switching]
![\includegraphics[scale=0.45]{fig/nakatnsw.eps}](img617.gif)
|
|
[Dependence on damping constant]
![\includegraphics[scale=0.45]{fig/nakatdamp2.eps}](img618.gif) [Dependence on damping constant for different particle sizes]
[Dependence on damping constant for different particle sizes]
![\includegraphics[scale=0.45]{fig/nakatdamping.eps}](img619.gif) [Temperature dependence]
[Temperature dependence]
![\includegraphics[scale=0.45]{fig/nakattemp.eps}](img620.gif)
|