


Next: 10.3 Interacting particles
Up: 10. Simulation of fine
Previous: 10.1 Cubic particles
Contents
10.2 Spherical particles
The mechanism of thermally activated magnetization switching in small spherical ferromagnetic particles has been investigated using the finite element model. The material parameters have been chosen as
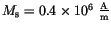 ,
,
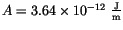 ,
, 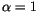 , and a radius
, and a radius
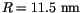 . The finite element mesh consists of 115 nodes and 440 elements. The mean diameter of the finite elements is 3 nm. This discretization is sufficient, if the we assume a rather low magnetocrystalline anisotropy. For
. The finite element mesh consists of 115 nodes and 440 elements. The mean diameter of the finite elements is 3 nm. This discretization is sufficient, if the we assume a rather low magnetocrystalline anisotropy. For
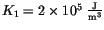 we find a typical domain wall width of
we find a typical domain wall width of
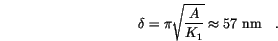
The initial magnetization is homogeneous and parallel to the easy axis of the particle. Its magnetization distribution is destabilized by an external magnetic field, which is parallel to the easy axis but antiparallel to the initial magnetization. Since this is a metastable state, we can expect the particle to overcome the energy barrier, which is called the activation energy, and reverse its magnetization after some time. In contrast to Monte Carlo simulations [58], we obtain not only information about the dynamical behaviour, but also about the switching times. The metastable lifetime (or relaxation time) 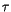 is defined as the time, which passes from the initially saturated state
is defined as the time, which passes from the initially saturated state
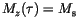 until
until 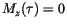 .
.
In order to measure the metastable lifetime a large number of simulations has been performed for each set of parameters. After 200 measurements a waiting time histogram was obtained (e.g. fig. ![[*]](../icons/crossref.gif) ). The integral of this histogram (or a cumulative histogram) is proportional to the switching probability
). The integral of this histogram (or a cumulative histogram) is proportional to the switching probability 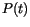 , that is the probability, that the particle has switched by a certain time (cf. fig.
, that is the probability, that the particle has switched by a certain time (cf. fig. ![[*]](../icons/crossref.gif) ). However, it is more common to draw graphs for the (rescaled) probability of not switching (fig.
). However, it is more common to draw graphs for the (rescaled) probability of not switching (fig. ![[*]](../icons/crossref.gif) )
)
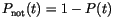 .
.
Figure:
Results of switching time measurements
[Switching time histogram]
![\includegraphics[scale=0.45]{fig/fem082210_01.eps}](img629.gif)
[Cumulative histogram]
![\includegraphics[scale=0.45]{fig/fem082210_02.eps}](img630.gif)
|
Figure:
Probability of not switching for different time step sizes
|
|
The magnetization reversal process can happen in different reversal modes. In a particle with low anisotropy the magnetization rotates coherently (figure ![[*]](../icons/crossref.gif) ), which means, that the magnetization remains almost homogeneous during the reversal process except for small thermal fluctuations. If the anisotropy is increased, it becomes favourable to form a nucleus with reversed magnetization. Thus, a droplet nucleates near the surface (figure
), which means, that the magnetization remains almost homogeneous during the reversal process except for small thermal fluctuations. If the anisotropy is increased, it becomes favourable to form a nucleus with reversed magnetization. Thus, a droplet nucleates near the surface (figure ![[*]](../icons/crossref.gif) ) and expands (figure
) and expands (figure ![[*]](../icons/crossref.gif) ) until the magnetization is completely reversed.
) until the magnetization is completely reversed.
Figure:
Magnetization reversal mechanisms in small spherical particles
[Coherent rotation]
![\includegraphics[scale=0.35]{fig/fem081001.eps}](img632.gif)
[Incoherent switching]
![\includegraphics[scale=0.35]{fig/fem081005.eps}](img633.gif)
[Colour map of 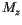 ]
![\includegraphics[scale=0.25]{fig/fem090711_scale.eps}](img634.gif)
|
Figure:
Nucleation of a droplet of reversed magnetization
[Droplet nucleation]
![\includegraphics[scale=0.30]{fig/fem081006_01.eps}](img635.gif)
![\includegraphics[scale=0.4]{fig/hinzke_ea.eps}](img636.gif)
[Droplet expansion]
![\includegraphics[scale=0.30]{fig/fem081006_02.eps}](img637.gif)
[Colour map of 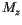 ]
![\includegraphics[scale=0.25]{fig/fem090711_scale.eps}](img634.gif)
|
The external field has been chosen to be comparable to the anisotropy field
Figure ![[*]](../icons/crossref.gif) shows, how the metastable lifetime decreases, when the external field is increased.
shows, how the metastable lifetime decreases, when the external field is increased.
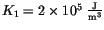 and
and
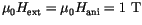 have been used at a temperature of 500 K. The negative sign indicates, that the external field is antiparallel to the initial magnetization. If we fit the data with the empirical law
have been used at a temperature of 500 K. The negative sign indicates, that the external field is antiparallel to the initial magnetization. If we fit the data with the empirical law
we can identify three different regimes with different slopes. At low fields (
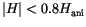 ) we find
) we find 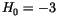 . Figure
. Figure ![[*]](../icons/crossref.gif) shows, that in this regime the magnetization switches coherently. For higher fields (
shows, that in this regime the magnetization switches coherently. For higher fields (
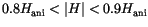 ) the fit results in
) the fit results in 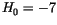 . The reason for the different behaviour is found in the different switching mechanism. The isosurface plot for
. The reason for the different behaviour is found in the different switching mechanism. The isosurface plot for 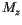 (fig.
(fig. ![[*]](../icons/crossref.gif) ) shows the nucleation of a reverse droplet. As it expands the magnetization is switched. Finally, a third regime is found for even higher fields (
) shows the nucleation of a reverse droplet. As it expands the magnetization is switched. Finally, a third regime is found for even higher fields (
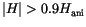 ). In this case the decay of magnetization is driven by several droplets, which nucleate independently at different places (fig.
). In this case the decay of magnetization is driven by several droplets, which nucleate independently at different places (fig. ![[*]](../icons/crossref.gif) ). The fit parameter is given by
). The fit parameter is given by 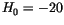 .
.
A similar behaviour has been observed in Monte-Carlo simulations [59], where this behaviour is interpreted in terms of droplet theory.
Figure:
Dependence of the metastable lifetime on the external field
|
|
Figure:
Coherent rotation of the magnetization at an external field of 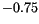 T
T
|
|
Figure:
Nucleation and expansion of a single droplet at an external field of 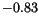 T
T
|
|
Figure:
Multi-droplet nucleation at an external field of 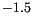 T
T
[Nucleation]
![\includegraphics[scale=0.5]{fig/fem090710_11.eps}](img656.gif)
[Expansion]
![\includegraphics[scale=0.5]{fig/fem090710_13.eps}](img657.gif)
[Droplets join each other]
![\includegraphics[scale=0.5]{fig/fem090710_15.eps}](img658.gif)
![\includegraphics[scale=0.4]{fig/hinzke_ea.eps}](img636.gif)
[Colour map of  ]
![\includegraphics[scale=0.25]{fig/fem090711_scale.eps}](img634.gif)
|



Next: 10.3 Interacting particles
Up: 10. Simulation of fine
Previous: 10.1 Cubic particles
Contents
Werner Scholz
2000-05-16
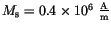 ,
,
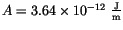 ,
, 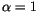 , and a radius
, and a radius
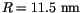 . The finite element mesh consists of 115 nodes and 440 elements. The mean diameter of the finite elements is 3 nm. This discretization is sufficient, if the we assume a rather low magnetocrystalline anisotropy. For
. The finite element mesh consists of 115 nodes and 440 elements. The mean diameter of the finite elements is 3 nm. This discretization is sufficient, if the we assume a rather low magnetocrystalline anisotropy. For
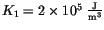 we find a typical domain wall width of
we find a typical domain wall width of
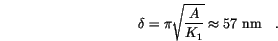
 is defined as the time, which passes from the initially saturated state
is defined as the time, which passes from the initially saturated state
 until
until 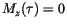 .
.
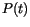 , that is the probability, that the particle has switched by a certain time (cf. fig.
, that is the probability, that the particle has switched by a certain time (cf. fig. 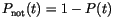 .
.
![\includegraphics[scale=0.45]{fig/fem082210_01.eps}](img629.gif) [Cumulative histogram]
[Cumulative histogram]
![\includegraphics[scale=0.45]{fig/fem082210_02.eps}](img630.gif)
![\includegraphics[scale=0.5]{fig/fem082210.eps}](img631.gif)
![\includegraphics[scale=0.35]{fig/fem081001.eps}](img632.gif) [Incoherent switching]
[Incoherent switching]
![\includegraphics[scale=0.35]{fig/fem081005.eps}](img633.gif) [Colour map of
[Colour map of 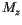 ]
]
![\includegraphics[scale=0.25]{fig/fem090711_scale.eps}](img634.gif)
![\includegraphics[scale=0.30]{fig/fem081006_01.eps}](img635.gif)
![\includegraphics[scale=0.4]{fig/hinzke_ea.eps}](img636.gif) [Droplet expansion]
[Droplet expansion]
![\includegraphics[scale=0.30]{fig/fem081006_02.eps}](img637.gif) [Colour map of
[Colour map of 
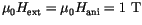 have been used at a temperature of 500 K. The negative sign indicates, that the external field is antiparallel to the initial magnetization. If we fit the data with the empirical law
have been used at a temperature of 500 K. The negative sign indicates, that the external field is antiparallel to the initial magnetization. If we fit the data with the empirical law

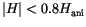 ) we find
) we find 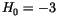 . Figure
. Figure 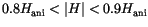 ) the fit results in
) the fit results in 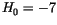 . The reason for the different behaviour is found in the different switching mechanism. The isosurface plot for
. The reason for the different behaviour is found in the different switching mechanism. The isosurface plot for 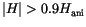 ). In this case the decay of magnetization is driven by several droplets, which nucleate independently at different places (fig.
). In this case the decay of magnetization is driven by several droplets, which nucleate independently at different places (fig. 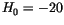 .
.
![\includegraphics[scale=0.5]{fig/fem082501_01.eps}](img647.gif)
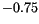 T
T![\includegraphics[scale=0.5]{fig/fem090712_6.eps}](img648.gif)
![\includegraphics[scale=0.5]{fig/fem090712_14.eps}](img649.gif)
![\includegraphics[scale=0.5]{fig/fem090712_23.eps}](img650.gif)
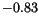 T
T![\includegraphics[scale=0.5]{fig/fem090711_19.eps}](img652.gif)
![\includegraphics[scale=0.5]{fig/fem090711_20.eps}](img653.gif)
![\includegraphics[scale=0.5]{fig/fem090711_23.eps}](img654.gif)
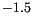 T
T![\includegraphics[scale=0.5]{fig/fem090710_11.eps}](img656.gif) [Expansion]
[Expansion]
![\includegraphics[scale=0.5]{fig/fem090710_13.eps}](img657.gif) [Droplets join each other]
[Droplets join each other]
![\includegraphics[scale=0.5]{fig/fem090710_15.eps}](img658.gif)