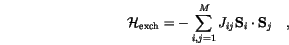
The Heisenberg Hamiltonian of the exchange interaction is usually written in the form
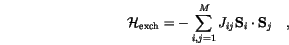
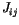 is the exchange integral, which can be calculated using quantum mechanics [11,12]. It decreases rapidly with increasing distance between the atoms, and so the sum has to be taken only for nearest neighbours and we can write
is the exchange integral, which can be calculated using quantum mechanics [11,12]. It decreases rapidly with increasing distance between the atoms, and so the sum has to be taken only for nearest neighbours and we can write 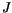 for
for 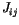 .
.
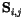 stands for the spin operators. If we replace them by classical vectors and rewrite the dot product, we obtain for the exchange energy
stands for the spin operators. If we replace them by classical vectors and rewrite the dot product, we obtain for the exchange energy
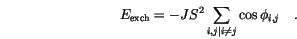
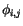 are small and develop the cosine into its Taylor series expansion. We also take the sum for each pair of nearest neighbours only once and redefine the zero level of the exchange energy by removing the constant term.
are small and develop the cosine into its Taylor series expansion. We also take the sum for each pair of nearest neighbours only once and redefine the zero level of the exchange energy by removing the constant term.
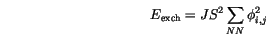
If we use the continuous variable
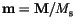 for the magnetization, we get for small angles
for the magnetization, we get for small angles
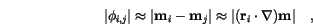
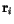 is the position vector from lattice point
is the position vector from lattice point 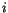 to
to 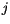 .
Then, the exchange energy is given by
.
Then, the exchange energy is given by
![\begin{displaymath}
E_\mathrm{exch}= J S^2 \sum_{i}\sum_{\mathbf{r}_i}
[(\mathbf{r}_{i} \cdot \nabla) \mathbf{m}]^2 \quad.
\end{displaymath}](img28.gif)
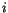 to an integral over the ferromagnetic body, we get
to an integral over the ferromagnetic body, we get
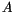 is given by
is given by

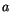 is the distance between nearest neighbours and
is the distance between nearest neighbours and
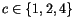 for a simple cubic, body centred cubic, and face centred cubic crystal structure, respectively.
for a simple cubic, body centred cubic, and face centred cubic crystal structure, respectively.