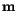 and the external field
and the external field 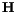 together with the temperature
together with the temperature 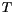 provide a complete characterization of states of our magnetic system. If
provide a complete characterization of states of our magnetic system. If 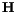 and
and
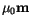 are conjugate work variables and
are conjugate work variables and 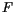 is the Helmholtz free energy, then
is the Helmholtz free energy, then
First, we assume, that the magnetic moment 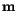 and the external field
and the external field 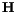 together with the temperature
together with the temperature 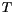 provide a complete characterization of states of our magnetic system. If
provide a complete characterization of states of our magnetic system. If 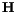 and
and
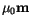 are conjugate work variables and
are conjugate work variables and 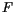 is the Helmholtz free energy, then
is the Helmholtz free energy, then
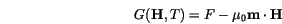 |
(2.1) |
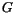 is the thermodynamic potential controlling spontaneous transformations under fixed
is the thermodynamic potential controlling spontaneous transformations under fixed 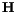 and
and 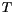 . Any transformation of this kind can only proceed in the sense of producing a decrease of
. Any transformation of this kind can only proceed in the sense of producing a decrease of 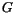 , and thermodynamic equilibrium is reached when
, and thermodynamic equilibrium is reached when 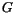 attains its globally minimum value. In our magnetic system the internal degrees of freedom, which give rise to these spontaneous transformations, can be represented by the magnetic moment
attains its globally minimum value. In our magnetic system the internal degrees of freedom, which give rise to these spontaneous transformations, can be represented by the magnetic moment 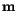 itself. Here, we assume, that
itself. Here, we assume, that 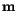 varies during the relaxation process and the internal processes leading to a certain value and direction of
varies during the relaxation process and the internal processes leading to a certain value and direction of 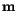 have characteristic relaxation times much shorter than the time scale over which
have characteristic relaxation times much shorter than the time scale over which 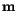 varies significantly and the system globally approaches equilibrium. This means, that the system relaxes by passing through a sequence of nonequilibrium states, each characterized by a well-defined value of
varies significantly and the system globally approaches equilibrium. This means, that the system relaxes by passing through a sequence of nonequilibrium states, each characterized by a well-defined value of 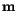 . The energy of these intermediate states, for fixed
. The energy of these intermediate states, for fixed 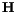 and
and 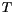 , is given by
, is given by
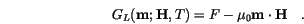 |
(2.2) |
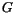 and
and 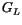 lies in the role of
lies in the role of 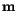 .
. 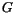 is a function of
is a function of 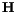 and
and 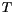 only, in which
only, in which 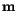 must be expressed as a function of
must be expressed as a function of 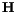 and
and 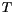 through the equation of state of the system. On the contrary,
through the equation of state of the system. On the contrary, 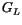 is the energy of that particular restriction where the state variable
is the energy of that particular restriction where the state variable 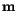 is forced to take a certain given value, as if it were an external constraint.
is forced to take a certain given value, as if it were an external constraint.
The equation of state of the system for the conjugate work variables 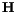 and
and 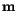 is given by
is given by
So far we did not consider the dependence of the magnetization on space coordinates, but magnetic materials exhibit complicated magnetization patterns. Thus, we subdivide our ferromagnetic body into many elementary volumes, which are small enough with respect to the typical length over which the magnetization varies significantly and at the same time large enough to contain a sufficient number of atoms, so that we can make use of statistical and thermodynamic methods to describe the properties of the volume. We can then calculate the Landau free energy for each elementary volume. At this point the different time scales become obvious again: The assumption, which led to the definition of 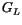 means, that the relaxation time over which individual elementary volumes reach thermal equilibrium with respect to the given local value of the magnetization
means, that the relaxation time over which individual elementary volumes reach thermal equilibrium with respect to the given local value of the magnetization
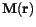 is much shorter than the time over which the system as a whole approaches equilibrium through time changes of
is much shorter than the time over which the system as a whole approaches equilibrium through time changes of
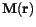 .
.
There are four important contributions to the Landau free energy of a ferromagnetic body: the exchange energy, the magnetocrystalline anisotropy energy, the magnetostatic energy, and the Zeeman energy in an external field [10].
Another contribution, magnetoelastic energy, which arises from magnetostriction, is omitted for two reasons. When a ferromagnet is magnetized it shrinks (or expands) in the direction of the magnetization. As a result, the volume changes and with it the saturation magnetization, which is defined as the magnetic moment in saturation per unit volume. However, in micromagnetics it is a basic assumption, that the saturation magnetization remains constant. Secondly, a large part of the internal magnetostriction in a ferromagnetic crystal can be expressed in the same mathematical form as magnetocrystalline anisotropy. If the anisotropy constants are taken from experiment, the effect of magnetostriction is already included, and therefore we do not have to consider it in an additional energy term.