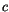 -axis. Experiments show, that it is symmetric with respect to the base plane, and so odd powers of
-axis. Experiments show, that it is symmetric with respect to the base plane, and so odd powers of 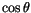 can be omitted in a power series expansion for the anisotropy energy density
can be omitted in a power series expansion for the anisotropy energy density
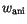 . The first two terms are thus
. The first two terms are thus
The Heisenberg Hamiltonian is completely isotropic, and its energy levels do not depend on the direction in space in which the crystal is magnetized. If there was no other energy term, the magnetization would always vanish in zero applied field. However, real magnetic materials are not isotropic. So the permanent magnets in microphones and loudspeakers do not lose their permanent magnetization after production. The most common type of anisotropy is the magnetocrystalline anisotropy, which is caused by the spin-orbit interaction of the electrons. The electron orbits are linked to the crystallographic structure, and by their interaction with the spins they make the latter prefer to align along well-defined crystallographic axes. Therefore, there are directions in space, in which a magnetic material is easier to magnetize than in others. The spin-orbit interaction can also be evaluated from basic principles. However, it is easier to use phenomenological expressions (power series expansions that take into account the crystal symmetry) and take the coefficients from experiment.
The magnetocrystalline energy is usually small compared to the exchange energy. But the direction of the magnetization is determined only by the anisotropy, because the exchange interaction just tries to align the magnetic moments parallel, no matter in which direction.
In hexagonal crystals the anisotropy energy is a function of only one parameter, that is the angle between the magnetization and the 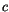 -axis. Experiments show, that it is symmetric with respect to the base plane, and so odd powers of
-axis. Experiments show, that it is symmetric with respect to the base plane, and so odd powers of 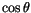 can be omitted in a power series expansion for the anisotropy energy density
can be omitted in a power series expansion for the anisotropy energy density
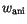 . The first two terms are thus
. The first two terms are thus
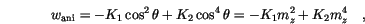
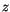 is parallel to the
is parallel to the 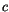 -axis. It is known from experiment, that terms of higher order, and in most cases even
-axis. It is known from experiment, that terms of higher order, and in most cases even 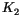 are negligible. If
are negligible. If 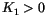 , then the
, then the 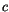 -axis is an easy axis, which means it is a direction of minimal energy. For
-axis is an easy axis, which means it is a direction of minimal energy. For 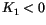 it is a hard axis with an easy plane perpendicular to it.
it is a hard axis with an easy plane perpendicular to it.