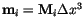 [24,25].
[24,25].
Another difficulty arises from the calculation of the demagnetizing field. Within each computational cell, the Wigner-Seitz cell of the lattice point, the magnetization is assumed to be homogeneous. We could now try to discretize Poisson's equation (![]() ) and Laplace's equation (
) and Laplace's equation (![]() ). The main difficulty arises from the open boundary conditions, which are discussed in section
). The main difficulty arises from the open boundary conditions, which are discussed in section ![]() . However, for a lattice of homogeneously magnetized cubes, it is possible to calculate the demagnetizing field analytically [23]. The expressions obtained are quite complex and computationally expensive to implement. Since the calculation of the demagnetization field by a magnetic scalar potential is very efficiently implemented in the finite element package, a third possibility has been chosen for the finite difference program. That is the approximation of the demagnetization field of each computational cell by the field of a magnetic dipole in the centre of the cell with the magnetic moment
. However, for a lattice of homogeneously magnetized cubes, it is possible to calculate the demagnetizing field analytically [23]. The expressions obtained are quite complex and computationally expensive to implement. Since the calculation of the demagnetization field by a magnetic scalar potential is very efficiently implemented in the finite element package, a third possibility has been chosen for the finite difference program. That is the approximation of the demagnetization field of each computational cell by the field of a magnetic dipole in the centre of the cell with the magnetic moment
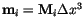 [24,25].
[24,25].
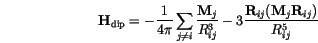
The contributions by the external field and the magnetocrystalline anisotropy to the effective field are straightforward, and they are all summarized in chapter ![]() .
.