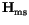 , has to be solved for a given magnetization distribution
, has to be solved for a given magnetization distribution
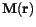 . We write Poisson's equation in a more general form
. We write Poisson's equation in a more general form
The solution of Poisson's equation (![]() ), which is required to calculate the demagnetizing field
), which is required to calculate the demagnetizing field
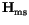 , has to be solved for a given magnetization distribution
, has to be solved for a given magnetization distribution
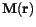 . We write Poisson's equation in a more general form
. We write Poisson's equation in a more general form
But first we have to define the vector spaces, in which we are searching for a solution [33]. Given a bounded domain 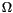 , we denote by
, we denote by 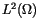 the space of quadratically integrable functions defined on
the space of quadratically integrable functions defined on 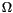 . The usual inner product
. The usual inner product
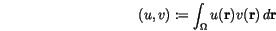
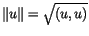 and
and 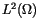 becomes a Hilbert space. The space
becomes a Hilbert space. The space 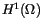 consists of those functions in
consists of those functions in 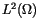 , whose (weak) derivative of order one also lie in
, whose (weak) derivative of order one also lie in 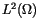 . The
. The 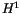 -inner product is defined as
-inner product is defined as
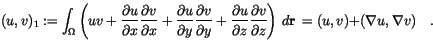
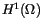 belongs to a family of function spaces known as Sobolev spaces. They can be physically interpreted as the space of functions of finite energy with respect to the problem under consideration. In this sense, it is the correct space in which to seek solutions of the weak formulation.
belongs to a family of function spaces known as Sobolev spaces. They can be physically interpreted as the space of functions of finite energy with respect to the problem under consideration. In this sense, it is the correct space in which to seek solutions of the weak formulation.
Further, we define the trial space 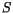
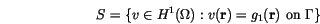
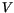
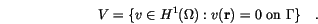
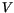 are called test functions.
are called test functions.
To derive the weak formulation we multiply Poisson's equation (![]() ) with a test function
) with a test function 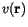 and integrate over the solution domain
and integrate over the solution domain
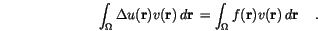
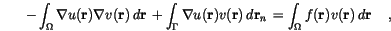
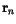 denotes the surface normal on the boundary
denotes the surface normal on the boundary 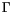 . If appropriate boundary conditions define the values of
. If appropriate boundary conditions define the values of 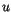 (Dirichlet boundary conditions) or of its derivatives
(Dirichlet boundary conditions) or of its derivatives 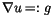 (Neumann boundary conditions) on the boundary, we can simplify (since
(Neumann boundary conditions) on the boundary, we can simplify (since 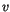 vanishes, where Dirichlet boundary conditions apply)
vanishes, where Dirichlet boundary conditions apply)
The variational formulation of (![]() ) can then be stated in the following general form: Find
) can then be stated in the following general form: Find 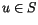 such, that
such, that
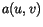 and the linear functional
and the linear functional 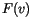 are given by
are given by
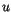 is sought, becomes equivalent to the test space
is sought, becomes equivalent to the test space 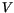 . Without loss of generality, we can thus assume that we seek the solution in the space
. Without loss of generality, we can thus assume that we seek the solution in the space 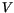 . It is noted, that the weak form is a generalization of the classical formulation. Therefore, the solution of the weak formulation need not be a classical solution at the same time.
. It is noted, that the weak form is a generalization of the classical formulation. Therefore, the solution of the weak formulation need not be a classical solution at the same time.
Not only Poisson's equation, but a large number of boundary value problems lead to symmetric and positive definite bilinear forms. Also for (![]() ) we find
) we find
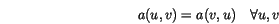
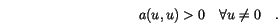
 is the sought solution, if it minimizes the functional
is the sought solution, if it minimizes the functional
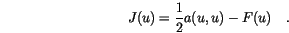
 can often be interpreted as an energy functional.
In the context of Poisson's equation for the demagnetizing field (
can often be interpreted as an energy functional.
In the context of Poisson's equation for the demagnetizing field (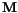 in the magnetic field
in the magnetic field 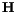
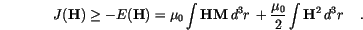
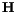 reduces
reduces 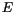 to the stray field energy
to the stray field energy 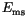 and makes
and makes 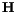 equal to the self demagnetizing field
equal to the self demagnetizing field
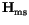 [34].
[34].
In general, the trial and test space 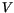 is too large and complex to deal with numerically. Thus, the Galerkin discretization seeks an approximation of the solution
is too large and complex to deal with numerically. Thus, the Galerkin discretization seeks an approximation of the solution 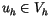 by restricting it to a finite dimensional subspace
by restricting it to a finite dimensional subspace 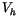 . We rewrite the weak formulation (
. We rewrite the weak formulation (![]() ) as follows: Find
) as follows: Find 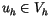 such, that
such, that
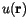 shall be approximated by a linear combination of trial functions
shall be approximated by a linear combination of trial functions
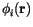 from a finite dimensional subspace
from a finite dimensional subspace 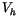 of
of 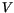
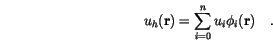
 lies in
lies in  , relation (
, relation ( . Conversely, if relation (
. Conversely, if relation (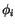 , then it also holds for all
, then it also holds for all 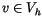 . Hence it is sufficient to determine the coefficients
. Hence it is sufficient to determine the coefficients 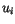 of
of 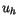 such, that
such, that
The finite element method is a particular Galerkin method [35], which uses piecewise polynomial functions to construct the finite dimensional subspace 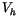 . The solution domain is divided into many small subdomains, referred to as elements. In two space dimensions these elements are usually triangles (fig.
. The solution domain is divided into many small subdomains, referred to as elements. In two space dimensions these elements are usually triangles (fig. ![]() ) or convex quadrilaterals, while in three dimensions tetrahedra, prisms and hexahedra are commonly employed. This subdivision process is usually called triangulation. The collection of all elements is referred to as the finite element mesh or grid.
) or convex quadrilaterals, while in three dimensions tetrahedra, prisms and hexahedra are commonly employed. This subdivision process is usually called triangulation. The collection of all elements is referred to as the finite element mesh or grid.
In the finite element method the basis functions
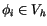 (fig.
(fig. ![]() ) are chosen in such a way, that
) are chosen in such a way, that
 of each basis function, i.e. the closure of the set, where
of each basis function, i.e. the closure of the set, where 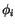 is nonzero, is small in the sense, that it consists of only a few (connected) elements. (fig.
is nonzero, is small in the sense, that it consists of only a few (connected) elements. (fig. 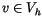 has a simple description in terms of
has a simple description in terms of 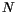 so called degrees of freedom which uniquely characterize
so called degrees of freedom which uniquely characterize 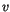 . Each basis function is characterized by possessing exactly one nonvanishing degree of freedom.
. Each basis function is characterized by possessing exactly one nonvanishing degree of freedom.
As the support is restricted to a very small local area, the integrals occurring in (![]() ) need only be computed over the small support of each basis function. In fact, most of the integrals are zero, and so the matrix of the linear system of algebraic equations is very sparse.
) need only be computed over the small support of each basis function. In fact, most of the integrals are zero, and so the matrix of the linear system of algebraic equations is very sparse.
|
[Support of basis function 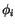 ] ]
![\includegraphics[scale=0.25]{fig/Ex1.5.eps}](img185.gif) [Support of basis function
[Support of basis function 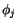 ] ]
![\includegraphics[scale=0.25]{fig/Ex1.6.eps}](img186.gif) [Common support of
[Common support of 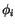 and and 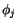 ] ]
![\includegraphics[scale=0.25]{fig/Ex1.7.eps}](img187.gif)
|